在实际问题当中碰到的随机型决策问题，往往是一类多阶段决策问题，这类问题在应用期望值准则作决策时，还可以借助于决策树的方法来解决.决策树就是将问题中有关策略、自然状态、概率及收益值等，通过线条和图形用类似于树状的形式表示出来.例如，图12－1就是例12－1决策问题的决策树.其中□表示决策点，由此引出的分支称为策略分支；○表示自然状态结点，由此引出的分支称为概率分支，分支旁标明的数字就是各个状态的概率；△表示决策终点，△旁所标的数字表示各个策略在相应的状态下的收益值；○上面的数字为相应策略的收益期望值.在图12－1的决策树中，策略S1的期望值最大，故选取S1.

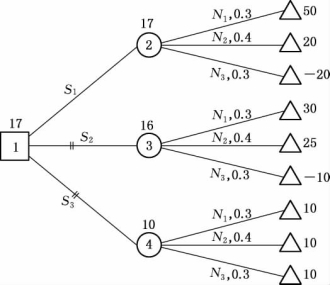
图12－1

借助于决策树，利用期望值准则作决策，具体步骤如下：

①绘制决策树：自左至右绘制；

②计算期望值：自右向左计算各策略的期望值，并将结果标在相应的状态结点处；

③选择策略：根据期望值最大准则从后向前进行“剪枝”决策，直到开始的决策点，选出期望值最大的策略.

例12－5　某化工厂原料车间，欲对旧工艺进行革新，采用新工艺.取得新工艺有两种策略：一是自行研究，成功的可能性为0.6；二是买专利，估计谈判成功的可能性为0.8.无论研究成功或谈判成功，生产规模都考虑两种方案：一是产量不变；二是增加产量.如果研究或谈判都失败，则仍采用旧工艺进行生产，并保持原产品产量不变.

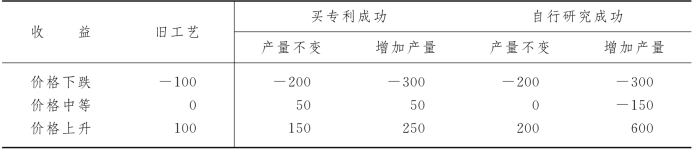
根据市场预测，估计今后几年内这种产品价格下跌的概率是0.1，价格中等的概率是0.5，价格上升的概率是0.4.经过分析计算，得到各个策略在不同价格的情况下的收益值，收益情况如表12－9所示.试用决策树方法寻找最优策略.

表12－9（单位：百万元）

解　（1）绘制决策树.如图12－2所示.

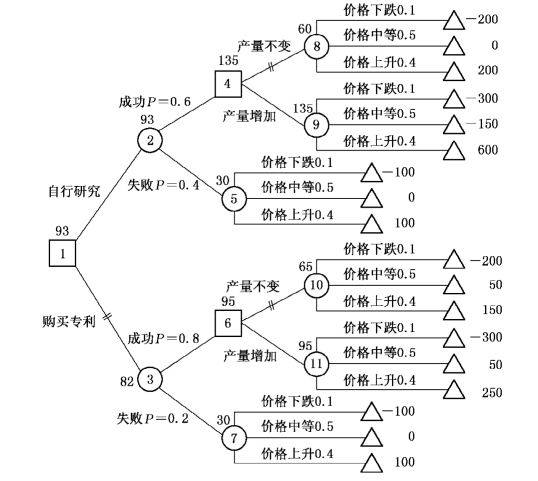
图12－2

（2）计算各结点的收益期望值.

结点⑧：E8＝（－200）×0.1＋0×0.5＋200×0.4＝60；(www.daowen.com)

结点⑨：E9＝（－300）×0.1＋（－150）×0.5＋600×0.4＝135；

结点⑩：E10＝（－200）×0.1＋50×0.5＋150×0.4＝65；

结点⑪：E11＝（－300）×0.1＋50×0.5＋250×0.4＝95；

结点⑤⑦：E5＝E7＝（－100）×0.1＋0×0.5＋100×0.4＝30.

因为结点④是决策点，通过以上计算可知，结点⑨的收益期望值大于结点⑧的收益期望值，所以决策点④的收益期望值取135，即采用增加产量的方案.同样，对决策点⑥，由于结点收益期望值大于结点⑩的收益期望值，所以决策点⑥的收益期望值取95，即采用增加产量的方案.

继续计算结点②，③的收益期望值：

结点②：E2＝135×0.6＋30×0.4＝93，

结点③：E3＝95×0.8＋30×0.2＝82.

（3）选择策略.通过比较后进行“剪支”，结点②的收益期望值大，所以应选取自行研究的方案.

例12－6　某电子厂根据需要对应用某种新技术生产市场所需的某种产品的生产和发展前景作决策.现有3种可供选择的策略：一是先只搞研究；二是研究与发展结合；三是全力发展.如果先只搞研究，有突破的可能性为60%，突破后又有两种方案：一是变为研究与发展结合；二是变为全力发展.如果研究与发展结合，有突破的可能性为50%，突破后有两种方案：一是仍为研究与发展结合；二是变为全力发展.无论采用哪一种策略，都将对产品的价格产生影响.据估计，今后3年内，这种产品价格下降的概率是0.4，产品价格上升的概率是0.6.

经过分析计算，得到各方案在不同的情况下的收益值，收益情况如表12－10所示.试画出决策树，寻找最优策略.

表12－10（单位：百万元）

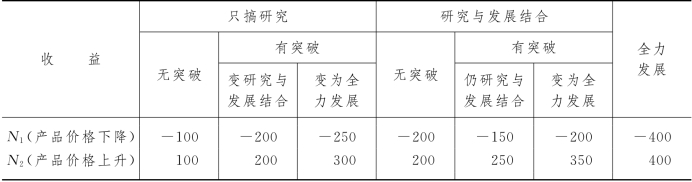
解　按照决策树方法，绘出决策树如图12－3所示.根据“决策树”图可知，应采用“研究与发展相结合，如有突破，再全力发展”的策略.