例12－1　某企业为了提高经济效益，决定开发某种新产品，产品开发生产需要对设备投资规模作决策.设有3种可供选择的策略：

S1：购买大型设备；　S2：购买中型设备；　S3：购买小型设备.

未来市场对这种产品的需求情况也有3种：

N1：需求量较大；　N2：需求量中等；　N3：需求量较小.

经估计，各种方案在不同的需求情况下收益值见表12－2.表中数据f（Si，Nj）出现负数，表示该企业将亏损.现问企业应选取何种策略，可使其收益最大？

表12－2

解　根据收益值表12－2，可以分别求出采用策略S1，S2，S3的效益期望值E（S1），E（S2），E（S3）：

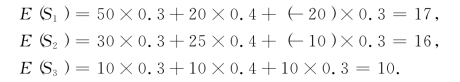
如果我们采用“收益期望值”最大作为决策的准则，那么就选取策略S1，即购买大型设备作为决策方案.

这种通过计算各个策略的收益期望值，按照大小作为决策标准的决策准则，我们称为期望值准则.期望值准则一般分两步：

①根据各种策略在不同的自然状态下的收益值和各种自然状态出现的概率，求出收益期望值E（Si），i＝1，2，…，m；

②比较收益期望值的大小作出决策.

例12－2　（设备更新问题）某工厂的大设备使用1 000个元件，元件寿命X（以月为单位）的分布如表12－3所示.如果元件单个更换，每只费用1.50元，若是全部一起更换，每只费用0.40元，请作出最优决策.

表12－3

解　元件寿命X的数学期望：

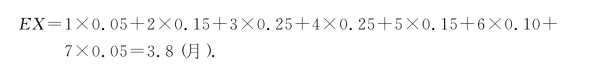
寿命期望值的倒数1／EX＝1／3.8为元件的损坏率0.263，它说明1 000个元件平均每月约需要更换263只，所以单个更换的方案平均每月的费用为

现在考虑一种更换方案，每m（m＝1，…，7）个月更换全部元件，同时在两次总更换之间各月损坏的元件也单个更换，其费用包括两类：

（1）每m个月1 000个元件更换的费用400元；

（2）在两次总更换之间的更换费用.

对于第二类费用，需要了解在两次总更换之间单个月的更换元件的平均数，这些数字可以在表12－4中得到.

我们来解释表12－4中数字产生的方法：

在第Ⅰ列中，在1月初（0月）有1 000个好元件，将1 000乘以元件寿命X概率分布P：

1 000×（0.05，0.15，0.25，0.25，0.15，0.10，0.05）＝（50，150，250，250，150，100，50），我们将这些各个月产生的损坏元件数字，填写在1 000数字下面，它们就是在相应7个月的更换平均数.

在第Ⅱ列，即在第二月，更换元件时，应该考虑在第一个月中更新的50个元件（带上括号）：

将这些数字填写在（50）下面，它们就是在相应后面7个月的更换平均数.在第Ⅲ列，即在第三个月更换的元件总数，为带括号的152.5，它是同一行中的两个数字150与2.5之和，即为1月、2月更换的元件总数.其他数字可用同样的方法得到.

表12－4

我们得到每m个月更换全部元件的费用如表12－5所示.(www.daowen.com)

表12－5

（说明：例如，取m＝3，策略为3个月全部更换一次，则两次总更换之间，被更换的元件数为50＋152.5＋265.5＝467.5.）

表12－5告诉我们，最优策略为两个月更换全部元件一次，期间坏一个更换一个.

例12－3　（存储问题）已知顾客对商店中某种食品每天需求量Nj的概率分布如表12－6所示.每出售一件食品，商店可获利2.5元；若当天卖不掉，每件食品将损失3.25元.试问商店对这种食品每日应进货多少？

表12－6

解　我们来计算需求量的期望值

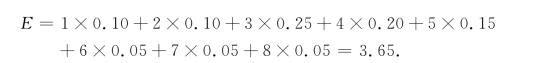
于是，我们采取3个策略：进货量分别取S1＝2，S2＝3，S3＝4.表12－7给出了这3种策略的期望值.所谓纯利润就是从出售的获利中减去因未能出售而遭受的损失，负的利润表示损失.

表12－7

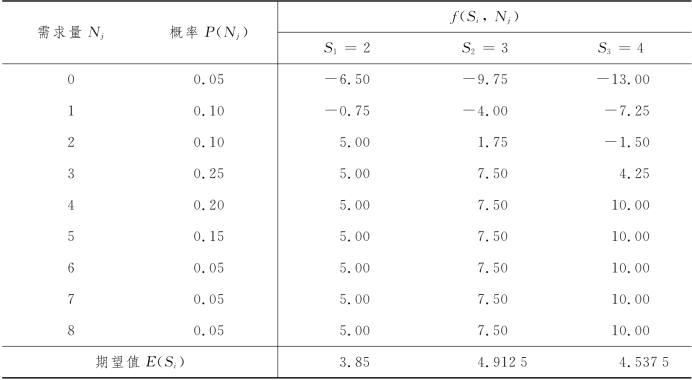
显然，最优策略为每天进货3件.

例12－3实际上就是存储论中著名的报童问题.我们对它再作进一步的讨论.不失一般性，我们给出报童问题如下.

例12－4　（报童问题）　报童每天要到邮局去订报，出售一份报纸可获得利润a（分），但如卖不出退回邮局，每份报纸要损失b（分）.根据以往经验，得知每天需求量为k份的概率为pk.问报童每天应订购多少份报纸，才能使他获利的期望值最大？

解　设报童每天订购的份数为n份，顾客每天需求量X是一个随机变量，于是，有P（X＝k）＝pk，报童每天的利润f（X）可用下列公式来表示：

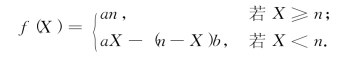
因此报童获利的期望值为

报童需要做出的决策：确定一个订购数n，使得E（f（X））最大.

我们采用边际分析法来求解报童问题例12－3，也即利用价格结构来检验和判断在什么情况下，再多订一份报纸是合算的.

假设报纸订购数取n份是合算的，现考察再多订一份报纸是否合算，也就是考察第n＋1件报纸的利润期望值.第n＋1份报纸售出时，获利为a分，售不出去时获利为（－b）分.因此，此时多订一份报纸的利润期望值为

其中p＝P（X≥n＋1）.所谓合算，就是利润期望值大于零.故由（a＋b）p－b＞0，可解得售出概率p应满足下述不等式：

表12－8

如果报童问题中的顾客每天需求量X是一个连续型随机变量，它的概率密度函数为f（x），则式（12－1）成为

满足此式的n＊即为报纸的最佳订购量.虽然n＊的值没有能够以显式的形式给出，但是如果概率密度函数知道了，便可通过计算或者查表得到n＊的值.

例如，a＝3，b＝1，现在x是［2 000，4 000］上均匀分布的连续型随机变量，它的密度函数为