例11-8 对例11-3,试问:
(1)若计算机在前一时段(15分钟)的状态为0,从本时段起,此计算机能够正常工作1小时的概率为多少?
(2)在运行比较长的时间后,计算机能够正常工作1小时的概率为多少?
解 由例11-3知:I={0,1},一步转移概率矩阵为
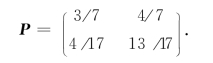
(1)可以认为初始阶段计算机处于状态0,经历4个阶段(1小时),计算机能够一直正常工作的概率为
![]()
(2)先来求稳态概率向量π=(π0,π1),我们有方程
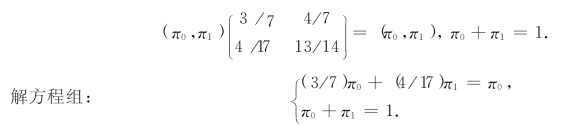
得到解π0=0.292,π1=0.708.于是,在运行比较长的时间后,计算机能够正常工作1小时的概率为(π1)4=(0.708)4=0.251.
例11-9 3家公司生产同一种产品,分别为A1,A2,A3.根据调查得知,各家产品去年12月在市场上占据的份额分别为50%,30%和20%.顾客购买的趋势可用下列转移概率矩阵(按照月来转移)来描述:

试问年底3家公司的产品在市场的占有率为多少?
解 现在I={1,2,3},Q0=(p1,p2,p3)=(0.5,0.3,0.2),P显然为正规转移概率矩阵.今年年底各公司占领市场的份额是Q12=Q0P(12),由式(11-13)知道,Q12近似于稳态概率向量π.求解方程组:
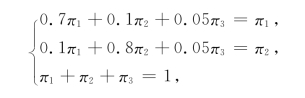
得到解π1=0.1765,π2=0.2363,π3=0.5882.年底3家公司的产品在市场的占有率分别为17.65%,23.63%,58.82%.也就是说,A1产品所占市场份额下降到17.76%.这种情况对于生产A1产品的公司来说情况堪忧.因此,除了提高产品质量外,应该考虑改进公司的销售策略.
一种策略是改进服务,争取将顾客的保留率p11提高到0.85,即让P变化为P′:

根据此矩阵求得的稳态概率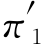 =0.316
=0.316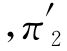 =0.263
=0.263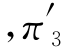 =0.421.
=0.421.
另一种策略是加强广告宣传,力图从另外两家公司那里把顾客争取过来.如果努力后P变化为P″:

根据此矩阵求得的稳态概率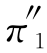 =0.333,π
=0.333,π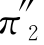 =0.222
=0.222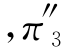 =0.445.
=0.445.
生产产品A1的公司,在运用马尔柯夫分析工具后,进行了适当的投资,以求进一步打开产品A1的销路.
例11-10 某公司每周检查一次产品的包装箱,状态分为“1”(指新包装箱)、“2”(指优等包装箱)、“3”(指良好包装箱)、“4”(指损坏的包装箱).如果包装箱处于状态4,就立即被拿去修理而更新成为新包装箱,时间需要一周.根据仓库的记录,货物包装箱状态转移概率矩阵为

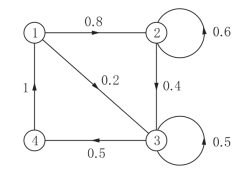
图11-3
被损坏的包装箱被拿去修理而更新为全新的包装箱,需要25元,但在检查时若发现一个包装箱被损坏而不能使用时,生产效率就要遭受价值18.5元的损失(延长了装货过程).
公司正在考虑另外一种策略:一旦检查员发现包装箱处于状态3,就拿去修理更新为新包装箱,于是就没有了状态4.问要不要采用这种新策略?
解 (1)如果采用旧方案,我们来求稳态概率向量π.由状态转移图图11-3可知P为正规转移概率矩阵,于是解方程组:
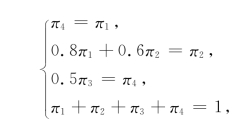
得到解:π1=1/6,π2=1/3,π3=1/3,π4=1/6.因此,每周新做包装箱与效率损失的期望费用为
![]()
(2)如果采用新策略,新状态转移概率矩阵为

解方程组:
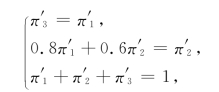
得到解: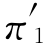 =1/4,
=1/4,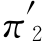 =1/2,
=1/2,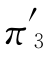 =1/4.此时,每周新做包装箱的期望费用(没有效率损失费)为
=1/4.此时,每周新做包装箱的期望费用(没有效率损失费)为
![]()
可见,采用新策略,比老方案可以节省1元.如果公司有包装箱6 000个,则可以节省相当一笔费用.
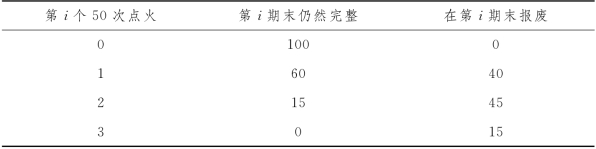
例11-11 工厂在厂内有100处安装使用某一型号的线圈.这些线圈用来点火,而且点火150次以后就完全报废.该工厂存储了足够的备品,以免中断生产.工厂线圈状态如表11-1所示,将该线圈进行个别更换时,费用为每个9元;将其全部更换时,每个5元,试问其更换之最佳策略.
表11-1
解 设第一个、第二个、第三个50次点火分别为状态1,2,3,则状态转移矩阵为

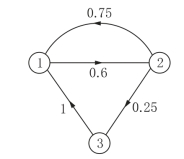
图11-4
例如,100个线圈在第一个50次点火后,由表11-1知,有40个报废,更换为新的,这40个线圈又可以进行第一个50次点火,所以p11=0.40,还有60个可以进行第二个50次点火,所以p12=0.60;60个线圈第二次50次点火后有45个报废,更换新的以后可以进行第一个50次点火,还有15个可以进行第三个50次点火,所以p21=45/60=0.75,p23=15/60=0.25;这15个线圈进行第三个50次点火后,完全报废,更换新的以后可以进行第一个50次点火,所以p31=1.
由状态转移图图11-4可知P是正规转移概率矩阵.现由(https://www.daowen.com)

得到方程组:
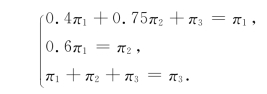
解之得到π1=0.57,π2=0.34,π3=0.09.于是有
![]()
就是说,若检查制度规定每当50次点火时对100个线圈进行检查,则在每次检查的时候,均有57个报废线圈需要更换,有34个可以在第二个50次点火时使用,有9个可以在第三个50次点火时使用.
为什么对π1=0.57进行这样的理解?我们应该逆向思维:由于π1=0.57,就是说有(100×0.57=)57个线圈在报废后进行了新线圈更换,才能处在第一个50次点火.这是理解马尔柯夫分析方法的困难之处.
表11-2

由表11-2可知,全体更换比个别更换能够节省费用,所以当全体线圈在第一个50次点火后,都进行更换,这是最佳策略.
例11-12 一个工厂每一季度都要对每个仪器进行检查,按照仪器状态分成5种:状态1“优秀”、状态2“良好”、状态3“及格”、状态4“可用”、状态5“不可用”.目前,工厂采用的维修策略(1)为:一旦仪器处在状态5,就被修理,使仪器达到状态1,费用为每台500元.根据统计资料,转移概率矩阵P为

工厂现在考虑维修策略(2):一旦仪器处在状态4和状态5,就被修理,使仪器达到状态1,每台费用分别为250元和500元.从长期的经济效益出发,最优维修策略是什么?
解 按照策略(1),由转移概率矩阵P,可求得
![]()
(请读者注意,为什么π1=π5?)
每个仪器维修费期望值为500×0.199=99.50(元).
按照策略(2),转移概率矩阵P′为

可求得:![]() =(0.266,0.228,0.241,0.168,0.097).
=(0.266,0.228,0.241,0.168,0.097).
(请读者注意,为什么![]() )
)
每个仪器维修费期望值为250×0.168+500×0.097=90.50(元).
因此,应该采用策略(2).
例11-13 设某机械制造厂定期检查机床轴承,把它们分为4级:状态1为“第一级新轴承”:状态2为“轻度磨损”;状态3为“中度磨损”;状态4为“报废”.更换一副新轴承,费用为50元.如果机床继续使用坏轴承运行,就可能发生故障,造成的损失费平均为250元(不包括更换轴承的费用).工厂采取更换策略(1):在每次检查中把处于状态4的轴承全部更换.根据统计资料,给出转移概率矩阵P如下:

工厂可以考虑采取更换策略(2):在每次检查中把处在状态3与状态4的轴承一起更换.试问哪种更换方式费用较小?
解 如果采用策略(1),则由转移概率矩阵P,求解方程组,经过计算可以求得
![]()
(请读者注意,为什么π1=π4?)
在更换现场,处于状态4的报废轴承将要更换为处于状态1的新轴承,新轴承与报废轴承并存在一起,各个的份额为0.15,报废轴承要拿走,所以实际上在平稳状态下,更换后的新轴承占留下的轴承份额为
![]()
这样一种思维问题的方法恐怕比较难以为初学的读者接受,这也是马尔柯夫分析方法被使用者掌握的困难之处.感谢这个案例的作者为我们留下这么一个值得令人学习的换位思维方法.不知道此处的文字是否已经说明了案例给出者的思维方法,从而能让读者完全接受与理解.
于是,在平稳状态下,每次换上的状态1的新轴承占全部轴承的0.177,换言之,对一副轴承来说,有17.7%的可能性要更换.所以对一副轴承来说,更换费与可能发生的故障费之和为
![]()
(在这里,作者理应指出,一般的读者比较容易理解例11-12处理问题的方法,把例11-13处理问题的方法列在例11-12后面,便于读者进行比较,以说明马尔柯夫分析在对问题的探讨上可以有不同的视角.)
如果采用策略(2),则状态就换成3个:状态1为“第一级新轴承”;状态2为“轻度磨损”;状态3为“中度磨损”与“报废”的轴承.转移概率矩阵P′如下:

求解方程组,可以求得稳态概率如下:
![]()
(请读者注意,为什么![]() ?)
?)
类似于我们在策略(1)中的解释,换上的新轴承占全部轴承的比率为
![]()
于是,以一副轴承为计算单位的更换费用如下:
(a)更换新轴承的费用:0.307×50元=15.35元;
(b)故障损失费:状态2占全部轴承的比率为0.530/(0.253+0.530)≈0.693,又根据转移概率矩阵P知道,状态2“轻度磨损”的轴承有10%的可能转变为状态4“报废”,因此故障损失费为
![]()
策略(2)的总费用为15.35元+17.325元=32.675元,显然,策略(2)比策略(1)好.如果该工厂使用这类轴承的数量比较大,可以节约相当的费用.
马尔柯夫分析是一个简单可行的决策方法,但是它对问题的思考与策略方案的理解是别具特色的,喜欢运用此方法的读者必须多看这方面的案例,不断积累经验,才能避免差错.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





