设矩阵P是一个均匀马尔柯夫链的一步转移概率矩阵，若是存在一个正整数k，使得矩阵Pk中每个元素均是正数，则称矩阵P是一个正规转移概率矩阵.

例11－7　试判断下列两个矩阵（状态集I＝｛1，2｝）是否是正规转移概率矩阵：

故矩阵B是正规转移概率矩阵，D不是正规转移概率矩阵.

判断一个转移概率矩阵是不是正规转移概率矩阵，也可以用状态转移图来进行分析.

例如，矩阵B与D的状态转移图分别如图11－1与图11－2所示.

图11－1

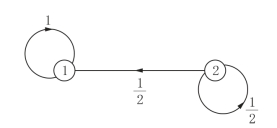
图11－2

在状态转移图中，顶点i代表状态，有向边（i，j）旁的参数表示转移概率pij.

显然，在图11－1中，状态1与状态2经过几步相互总能到达.如状态1虽然一步不能到达状态1，但是状态1可以到达状态2，然后状态2可以到达状态1，即状态1经过两步可以到达状态1.所以B是正规转移概率矩阵.而在图11－2中，状态1永远不能到达状态2.

所以，判断一个转移概率矩阵是否是正规转移概率矩阵，只要用它的状态转移图就可以进行判别.如果状态集中任意两个状态总是能够相互到达（不管几步），那么，这个矩阵就是正规转移概率矩阵.(www.daowen.com)

定理11－2　如果一个均匀马尔柯夫链（状态集I＝｛1，…，m｝）的一步转移概率矩阵是正规转移概率矩阵P，则唯一地存在一个稳态概率向量π＝（π1，…，πm），它是由下列方程组给出的解：

这里要指出，πP＝π虽然有m个方程，但是只有m－1个方程是独立的（因为把这m个方程加起来，得到一个恒等式），而变量却有m个.于是，我们在式（11－9）中任意选取m－1个方程，与式（11－10）一起组成m个方程，就能够求解m个变量.

向量π＝（π1，…，πm）称为稳态概率向量，概率πi称为状态i的稳态概率.

式（11－12）告诉我们，P（n）随着幂次的增大，P（n）的第i列元素趋向一个同样的值πi.这说明经历一定时间的状态转移后，初始状态的影响逐渐消失，系统最终达到完全与初始状态无关的一种平稳状态.

我们还有如下结论：

（1）假设有k个相互独立的均匀马尔柯夫链，在相同的转移概率矩阵下进行状态转移，那么在经历一段长时间运行后处于状态i的过程的个数的期望值为kπi.

（2）概率πi也给出在一个长时间内过程处于状态i的次数占整个转移次数中的比率.

（3）数1／πi为自状态i出发首次回复到状态i所需要的转移次数的平均值.