（q，Q）策略的基本内容是：对库存水平进行连续检查，当库存水平减少到订购点q以下时，提出订购量为Q的订货请求，经过拖后时间L后，数量为Q的货物一定入库.应用该策略的存储模型需要寻求订货点q和订购批量Q.这个存储模型具有下列几点基本假设.

（1）拖后时间L（L＞0）为固定常数.在拖后时间内，需求量为随机变量X，其概率密度函数r（x）为已知，且数学期望E（X）＝μ.

（2）在拖后时间L结束前，当实际需求量超过q时，允许出现缺货现象.当库存量减少到零以后，将未能满足需求的缺货累积起来，待到货后再补交，也就是说它为缺货有预约.

（3）每次订购费为a，单位时间内单位货物的存储费为b，单位时间内单位货物的缺货费为c.

该模型存储状态变化如图10－7和图10－8所示.

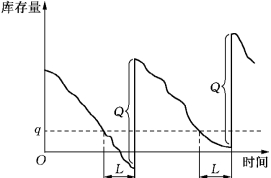
图10－7

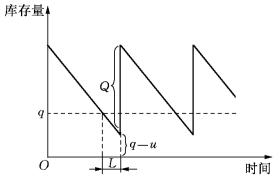
图10－8

从图10－7可以看出，虽然每次的订货批量Q及拖后时间L均保持不变，但相继两次补充的时间间隔t却并不一定相等.同时可以看到，补充进货后的库存水平也不一定相等.

我们来考虑单位时间内货物存储的平均总费用f.显然，同前面模型一样，

由于模型中存在随机变量，所以我们关心f的数学期望E（f）.

如果假设单位时间需求量为随机变量u，则u的数学期望E（u）与拖后时间L内需求量X的数学期望E（X）＝μ之间有如下关系式μ＝LE（u）.

现每次订货批量为Q，则单位时间订货次数的期望值为E（u）／Q＝μ／（LQ），于是单位时间订购费的数期望值aμ／（LQ）.

从存储状态图10－7中可以看出，缺货情况只可能出现在拖后时间L这段时间内，而这段时间开始时有存货量q，实际需求量为随机变量X，因此缺货量也为随机变量，则当X≤q时，缺货量为零；当X＞q时，缺货量为（X－q），则在拖后时间L内缺货量的期望值为

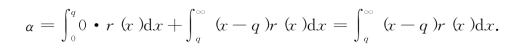
因为单位时间内订货次数的期望值为μ／LQ，则单位时间内缺货费用的期望值为cαμ／（LQ）.

存储费用的分析同确定型模型相似.由图10－8知，在订货周期t内的存储量为一个梯形面积.该梯形的左边边长的期望值为Q＋q－μ，梯形的右边边长的期望值为q－μ，因此，梯形的面积为（Q＋q－μ＋q－μ）t／2.于是单位时间存储费的期望值为e（Q／2＋q－μ）.

从而，我们求得单位时间内货物存储的总平均费用的期望值

(www.daowen.com)

与前面方法相同，将上式分别对q和Q求一阶偏导，令其等于零，解方程组得：

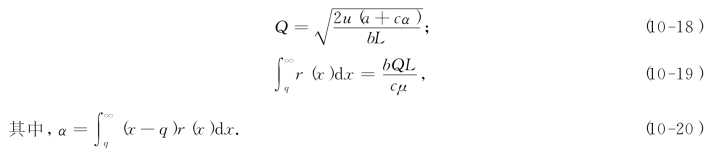
但是，在Q和q的计算公式中，因包含有相互关联的未知量，而不能直接求出最终结果，为此采用逐步逼近的迭代法求解.具体算法步骤如下.

①令α0＝0，Q0＝＋∞，q0＝＋∞，k＝1；

②取α＝αk－1，代入式（10－18），计算Qk；

③取Q＝Qk，代入式（10－19），计算qk；

④取q＝qk，代入式（10－20），计算αk；

⑤判断｜Qk－Qk－1｜＜ε1，｜qk－qk－1｜＜ε2是否成立？

若是，则Qk和qk即为所求的最优订购批量和最优订购点，算法终止；

若否，则取k＝k＋1，转步骤②继续计算.

在这个算法中，α的计算比较困难.在实际问题中，拖后时间L内的需求量X多数服从正态分布N（μ，σ2）.不失一般性，我们给出正态分布情况下α的计算方法.

由概率论知，若随机变量Y服从正态分布N（0，1），概率密度函数为φ0（x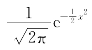）＝，分布函数为Φ0（x）；随机变量Z服从正态分布N（μ，σ2），概率密度函数为

在Q给定并计算（1－d）后，通过查表求得q.

例10－7　某宾馆与一家饮料公司签订了长期订购瓶装矿泉水的合同.合同规定，每次订货的提前时间为3天，在此之间，宾馆的需求呈正态分布，其均值为1 000瓶，标准差为250瓶.一次订货的手续费为100元，存储费用是每月每瓶0.15元，假定拖后时间内的缺货在下次到货后要补齐，缺货损失费用为每瓶1元.试根据上述条件确定最佳订货批量和最佳订货点（假定一个月为30天）.

解　本问题的单位时间为月.由已知条件可知：μ＝1 000瓶，σ＝250瓶，L＝0.1月，a＝100元，b＝0.15元，c＝1元.

迭代至此结束，因为Q3和q3的变化都已相当小.所以，我们取最佳订购批量Q＊＝3 760瓶，最佳订购点q＊＝1 370瓶.

事实上，由于需求的变化受到社会、经济等多种因素的综合影响，常常独立于人们的主观控制能力以外，因此其在数量上、时间上一般无法精确确定，而其呈现出的随机性却使库存控制变得复杂和困难.所以，为了探讨研究存储问题的方法，为了提炼存储问题中共同的、本质的内容，本章所介绍的确定型和随机型存储问题中的基本模型，都是在一定的假设条件下进行探讨的，这样的条件在现实生活中是比较难以找到的，应用时要根据问题的实际背景加以修正.经过数学抽象和概括的存储模型，虽然不可能与实际存储问题完全等同，但是对于模型的探讨会加深对存储问题的认识，模型的求解可以为存储系统的决策提供定量依据.