现在我们假设供需过程可以分成若干阶段（每个阶段的时间长度相同，例如1个月或者1周），拖后时间L为零，每个阶段对存储货物的需求量u是一个随机变量.如果对于不同的阶段来说，销售、需求只是一种重复性的活动，我们就只要研究一个阶段的存储问题就可以了，因此称它为单阶段的随机存储模型，采用（s，S）策略.

现设u是一个离散型的随机变量，它取的数值分别为0≤i1＜i2＜…＜im.u的概率分布为

自然，应有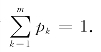

在每阶段初检查库存，若发现库存量低于规定的数量s，就立即补充货物并把库存量提高到规定的数值S.在下面讨论中，我们就以一个阶段的时间长度作为单位时间.

1.S值的确定

设在阶段初未进货时的库存量为g，阶段初补充的数量为Q，因而补充后的库存量y＝g＋Q.假设这阶段的存储费按这阶段末的库存量来计算，我们就可算得这阶段存储费的期望值为

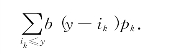
假设这阶段缺货损失费也按这阶段末的缺货量来计算，于是我们可算得这阶段缺货损失费的期望值为

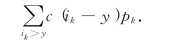
因此，这个阶段（单位时间）内总费用的期望值为

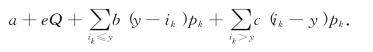
我们采用边际分析法来确定S的值.现设阶段初进货后库存量为y件是合理的，我们来分析一下再多进一件货物而使库存量为y＋1件的合理性.对于多进的这一件货物，实际需要用它的概率为1－，费用为购置费e；实际不需用它的概率为，费用为购置费e与存储费b之和e＋b.所以多进这件货物的费用期望值为

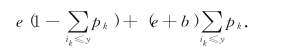
若不多进这件货物，则需承担的缺货费的期望值为

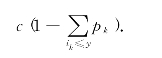
所谓多进一件货物是合理的，是指相应的费用期望值小于不进这件货物时的费用期望值，即

也就是

因此，S应是满足上述不等式的最大的y值再加1，或者是满足下列不等式的最小的y：

(www.daowen.com)

但是u的取值集合为｛i1，…，ij，…，im｝，故y应取满足上述不等式的最小ij.

2.s值的确定

设阶段初库存量为y，而且决定不进货.于是，当这阶段的实际需要量低于y时，要支付存储费；当实际需要量高于y时，要承担缺货费.因而这阶段内总费用的期望值为

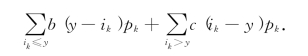
若阶段初库存量为y，现决定补充货物，把库存量提高到S.这时，这阶段总费用的期望值为

若不进货时的费用期望值小于进货时的费用期望值，即下列不等式成立，则不进货是合理的：

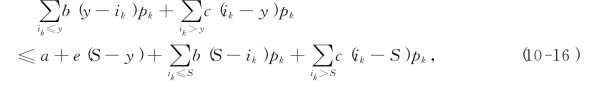
所以s为满足下列不等式的最小y值：

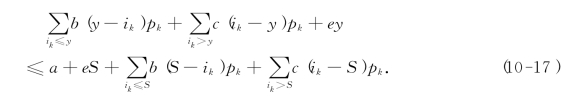
这一计算s值的公式虽比计算S的公式复杂些，但并非像看上去的那样困难.当S确定后，该不等式右端的数值即可求得.不难发现，当y＝S时，该不等式一定成立，故这个不等式的解总存在.我们对y＝i1，y＝i2，…，y＝S逐个计算该不等式左端的值，并与右端的值进行比较，使不等式成立的最小y值就是s.

例10－6　某企业对于某种材料每月需求量的概率分布如表10－1所示.每次订货费为60元，每月每吨存储费为40元，每月每吨缺货费为1 015元，每吨材料的购置费为800元.该企业欲采用（s，S）策略来控制库存量，请求出s和S的值.

表10－1

解　先建立表10－2.

表10－2

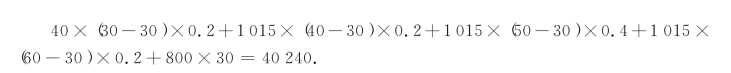
因为40 240＜40 260，所以s＝30.即该企业采取（30，40）策略.

在实际使用这种存储策略时，如存储量不易清点，因而实际存储量很难随时得知时，可将存储货物分两堆存放.一堆数量为s，其余的另放一堆.平时从后一堆取货以满足需求.当后一堆取完，需要动用前一堆时，期末就订货；如至期末，前一堆仍未动用，则本阶段不订货.因此，这种存储策略俗称双堆法（或两堆法）.