
在有些情况下,存储系统允许缺货现象存在.在存储水平变为零以后,还要等一段时间后再去订货,此时,由于缺货就要带来一定的缺货损失费.但是,该存储系统库存量比不允许缺货时要少,从而存储费相对就可节省,同时,不必经常地去订货,也会使订购费用减少.当降低的成本大于造成的缺货经济损失时,存储系统自然就采取缺货的策略了.
这个存储模型的基本假设前提是:
(1)当库存量减少到零时,延迟一段时间再进行补充.但一旦进行补充,瞬时就能到货,补充一次性完成;
(2)需求均匀连续,需求速率u为常数,在订货周期t内的需求量为ut,每次订购批量Q,有Q=ut;
(3)每次订购费a相同,单位时间内单位货物的存储费b不变,单位货物的缺货费c不变.
该模型的存储状态变化如图10-3所示.
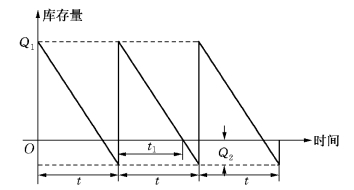
图10-3
如图10-3所设,每一个订货周期t内的最大缺货量为Q2,实际进库量为Q1,当进货时,每批的订购批量为
![]() (www.daowen.com)
(www.daowen.com)
在这里,我们假定采用“缺货预约”的办法:未能满足的需求量作为缺货予以登记,待进货后立即进行补偿.或者在实际问题中也可以如此处理:该存储系统有一个安全库存量Q2(需要支付超存储费,也即缺货损失费),一旦缺货就动用安全库存量Q2.当进货时,被动用的安全库存量Q2应该得到补偿.
同前面一个模型一样,我们设单位时间内存储货物总费用的平均值为函数f.在订货周期t内总费用为订货费、存储费与缺货费之和.
根据假设,单位时间的订货费为eu+(a/t).
由图10-3可知,在订货周期t内的存储量为一个三角形的面积:Q1t1/2,因此,单位时间内的存储费为bQ1t1/(2t).在订货周期t内的缺货量为一个三角形的面积:Q2(t-t1)/2,因此,单位时间内的缺货费为c Q2(t-t1)/(2t).根据相似三角形对应边关系,有(t-t1)/t=Q2/Q,又Q=ut,Q2=Q-Q1,故单位时间内的缺货费为c(ut-Q1)2/(2ut).
综上所述,单位时间内存储货物的平均总费用函数为

例10-3 若在例10-1中,其他条件不变,现可以考虑允许缺货,每月的缺货损失费c为1.5元/件.试计算这时的最佳订购批量、最佳订货周期、最小平均费用.
解 根据式(10-6)、式(10-4)和式(10-8),可得:
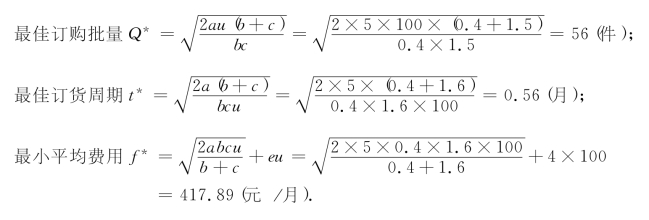
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







