M／M／S／m／m是顾客源有限的排队模型，即至多只有有限个（m个）顾客来到服务系统.一旦系统中已有m个顾客，就不会再有新顾客到达，除非系统中的一些顾客得到服务又返回顾客源，系统才可能有顾客继续到来（参看图9－8）.

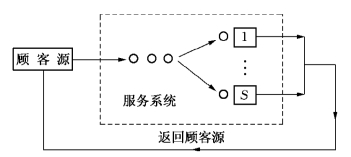
图9－8

有限源服务系统的典型例子是机器看管问题.假定有S个工人共同看管m台机器（m≥S，m台机器就是顾客源）.每当机器发生故障时，就需要有一位工人负责修理，使其恢复生产.所以，出故障的机器就是要求获得服务的顾客，工人就是服务台.当S个工人分别正在修理m台出故障的机器时，新发生故障的机器就只能等待工人来修理.我们假定：

（1）每台机器连续正常运转时间都服从参数为λ的负指数分布，每台机器平均连续运转的时间为1／λ，λ就是一台机器在单位运转时间内发生故障的平均次数（应注意，λ不是一台机器单位时间内发生故障的平均次数，因为一台机器一旦发生了故障，在修复之前不会再发生故障）.

（2）每台机器的修复时间都服从参数为μ的负指数分布，工人修理一台机器的平均时间为1／μ.

（3）各台机器在任意时段内连续运转的时间与工人修复机器的时间彼此独立.

若以ξ（t）表示在时刻t不在正常运转的机器数，它是一个随机变量，因而｛ξ（t）｜t≥0｝是一个随机过程，它的状态集合为有限集I＝｛0，1，…，m｝.可以证明，｛ξ（t）｜t≥0｝为一个生灭过程，其状态转移图如图9－9所示.所以，对该生灭过程来说，有

图9－9

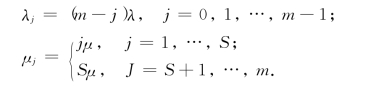
于是，根据定理9－3便可得到系统的稳态概率：

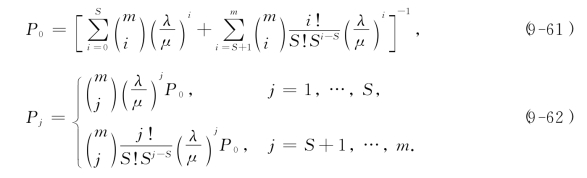
（由于P0，Pj计算公式过于复杂，有专书列成表格可供使用.）由此我们即可计算L，Lq及D：

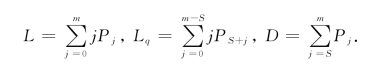
有效到达率λe的计算公式为：

直观上可以如此来理解该公式：每台机器在单位运转时间内发生故障的平均次数为λ，而系统外平均只有m－L台机器在运转，所以m台机器在单位时间内实际发生故障的平均次数λe＝λ（m－L）.

应用李特尔公式和式（9－63），即可计算W和Wq.(www.daowen.com)

特别当S＝1时，有

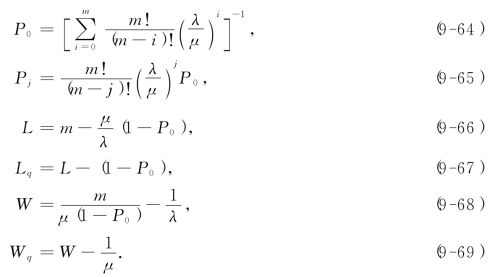
例9－21 4名工人看管10台机器，每台机器平均每运转30分钟就要修理一次，每次修理平均需要10分钟.设机器连续运转时间和修理时间均为负指数分布.求：

（1）需要修理的机器平均数；

（2）一分钟内10台机器平均出现故障的次数；

（3）机器的平均停工时间.

解　本问题为M／M／4／10／10排队模型，现在λ＝1／30，μ＝1／10，λ／μ＝1／3.经计算，稳态概率分别为

例9－22　某厂有若干台机器，它们连续工作时间服从同一参数λ的负指数分布.工人修理时间服从同一参数μ的负指数分布.设λ／μ＝0.1.今有两个方案：方案Ⅰ为3个工人各自独立看管机器，每人看管6台机器.方案Ⅱ为3个工人共同看管20台机器.试比较两个方案的优劣.

解　方案Ⅰ为M／M／1／6／6模型，λ／μ＝0.1，经计算可知系统的稳态概率为

事实上我们能证明如下一般的结论：系统M／M／S／Sm／Sm的服务要比S个M／M／1／m／m系统来得好.它的直观解释是：当S个工人各自独立看管m台机器时，工人甲单独看管的m台机器，某个时候可能同时有多于一台的机器发生故障，他只能在一台机器上排除故障，其他停止运转的机器只能停产等待修理；但可能另一个工人乙看管的m台机器，这时全处于正常运行，如是共同看管，则这时工人乙就可去排除由工人甲看管的等待修理的机器的故障.

例9－23　设在工人看管机器问题M／M／1／m／m模型中，我们可以采用不同的工艺和设备来检修机器.工艺和设备先进，服务率μ增大，但相应的检修费用也增大.设单位时间检修费为服务率μ的函数C5μ（C5为一常数），每台正常运转的机器单位时间可获利C6，试确定最优服务率μ＊以使系统在单位时间内获得的纯利润最大.

解　由于单位时间内正常运转的机器平均台数为m－L，由式（9－66）知

所以，单位时间内系统的纯利润f为

求f的极值，即可求得最优服务率μ＊.