M／M／S／k排队模型为泊松输入、负指数分布服务、S个服务台、系统容量为k的混合制系统（S＜k）.

假定参数为λ的最简单流到达S个服务台的系统，若顾客到达时有空闲的服务台，则顾客在任一个空闲服务台接受服务，服务时间与到达间隔相互独立，遵从参数为μ的负指数分布；若顾客到达时所有S个台都在进行服务，则当系统中的顾客数（包括正在服务的S个顾客）小于指定数k时，新来的顾客就排入队伍等待，而当系统中的顾客数等于k时，新来的顾客就被拒绝而损失.

若ξ（t）为在时刻t时系统内的顾客数，则｛ξ（t）｜t≥0｝是一个随机过程，可以证明它是一个状态集为有限集I＝｛0，1，…，k｝的生灭过程.其状态转移图如图9－7所示.所以，对该生灭过程来说，有

图9－7

例9－16　两位理发师经营的理发馆有5把椅子供顾客排队等待使用.当5把椅子都坐满时，后来的顾客就不再进入理发店而离开.假若顾客流为最简单流，平均到达率为3.763 4顾客／小时，顾客理发时间为负指数分布，平均需要15分钟.求：

（1）顾客一到理发店就能理发的概率；

（2）等待理发的顾客的平均数；

（3）有效到达率；

（4）一位顾客在理发店内预期花费的时间；

（5）在可能到达的顾客中不等待就离开的顾客的百分比.

解　本问题为M／M／2／7排队模型，S＝2，k＝7.现在λ＝3.763 4，μ＝4，ρ＝0.47.

（1）这相当于求理发店内不多于一位顾客的概率P0＋P1.经计算可知P0＝0.361 33，P1＝0.339 96，于是

例9－17　某汽车加油站只有一台加油泵，且场地至多只能容纳3辆车，当站内场地占满车时，到达的汽车只能去别处加油.输入为最简单流，每8分钟一辆，服务为负指数分布，每4分钟一辆.加油站有机会租借毗邻的一块空地，以供多停放一辆前来加油的车，租地费用每周120元，从每个顾客那里期望净收益10元.设该站每天开放10小时，问租借场地是否有利？

(www.daowen.com)

所以，租借场地是合算的.

例9－18　现有M／M／1／2服务系统，其平均到达率λ＝10人／小时，平均服务率μ＝30人／小时.管理者想增加收益，拟采用两个方案：方案A为增加等待空间，取k＝3；方案B为提高平均服务率，取μ＝40人／小时.设对每个顾客服务的平均收益不变，问哪一个方案将获得更大的收益？当λ增加到每小时30人，又应采用哪一个方案？

解　由于对每个顾客服务的平均收益不变，因此，服务机构单位时间的平均收益，与单位时间实际进入系统的顾客平均数λe成正比.所以本问题即为比较两个方案的有效到达率λe.

（1）方案A为M／M／1／3排队模型：

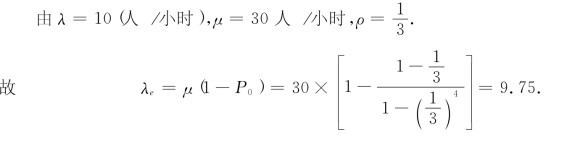
可见，当λ＝30人／小时时，应采用方案B.

例9－19　若M／M／1／k排队模型的平均服务率可以调整，服务台提供服务的费用每单位时间为C1μ元，每服务一位顾客可收益C4元，求最优服务率μ＊.

解　由于有效到达率λe＝μ（1－P0）为单位时间实际进入服务机构的顾客平均数，那么，在稳定状态下，它也等于单位时间内实际服务完的顾客平均数.因此在单位时间内系统的纯利润

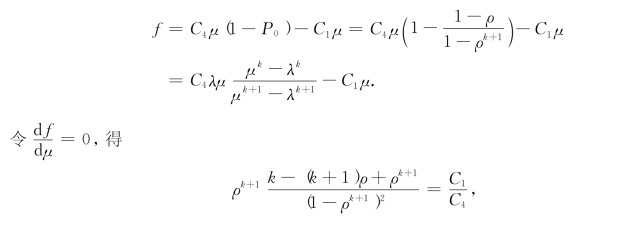
此方程的解即为最优解μ＊.

当k＝S时，作为M／M／S／k的特例，我们得M／M／S／S排队模型，它是损失制的服务系统，若顾客到达时S个服务台都正在进行服务，则该顾客就自动离去并不再回来.这时，有关的计算公式如下：

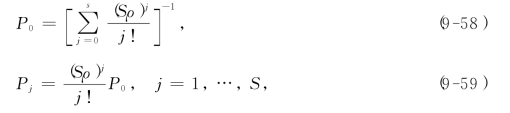
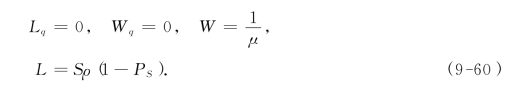
L即为系统中正在服务的服务台期望值.PS为S个服务台均被占用的概率，即顾客到达时遭到拒绝的概率（损失率）.

例9－20　设某火车站的电话问讯处有3架电话，可以看作为一个M／M／3／3服务系统，平均每隔2分钟有一次问讯电话（包括接通的和未接通的），每次通话的平均时间为3分钟.试问打到问讯处的电话能接通的概率为多少？

因此，接通的概率为1－P3＝0.866.