【摘要】:解本问题为M/M/∞排队模型.现在λ=6,=0.5,因此ρ=3.所以正在卸货的平均作业队数L=3.而需要7个以上作业队卸货的概率
M/M/∞为泊松输入、负指数分布服务、无限个服务台的服务系统.
假定参数为λ的最简单流到达无限个服务台的系统,则顾客一到达立即就可接受空闲着的服务台的服务.服务时间与到达间隔相互独立,服务时间是参数为μ的负指数分布.
若系统在时刻t时正在进行服务的服务台台数为j,我们就说在时刻t系统所处的状态ξ(t)=j,其状态集I={0,1,2,…}.
可以证明{ξ(t)|t≥0}为一个生灭过程,其状态转移图见图9-6.所以,对该生灭过程来说,有
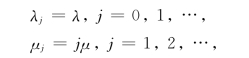
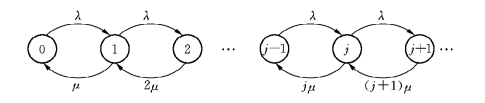
图9-6
此时定理9-3的条件(9-4)总成立,则由式(9-8)和式(9-9)得:(https://www.daowen.com)
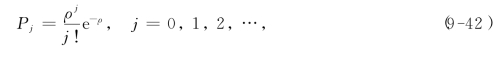
其中ρ=![]() .于是,可知系统中在服务的服务台平均数
.于是,可知系统中在服务的服务台平均数
![]()
例9-15 某航运公司有一个装卸码头,外轮按最简单流到达,平均每天有6艘船到达.每艘船的卸货时间服从负指数分布,每个装卸作业队平均每天卸船2艘.由于外轮在港内停留时间超过期限罚款极重,因此公司成立了较多的装卸作业队,基本上使外轮一到码头就能得到服务,问正在工作的装卸作业队平均数为多少?需要7个以上装卸作业队工作的概率为多少?
解 本问题为M/M/∞排队模型.现在λ=6,![]() =0.5,因此ρ=3.所以正在卸货的平均作业队数L=3.而需要7个以上作业队卸货的概率
=0.5,因此ρ=3.所以正在卸货的平均作业队数L=3.而需要7个以上作业队卸货的概率
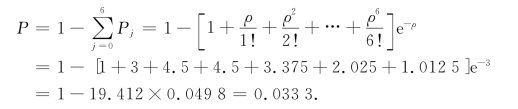
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







