M／M／1排队模型为M／M／S在S＝1时的特例.现设

由式（9－22）和式（9－23）可知

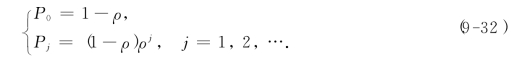
因此，有

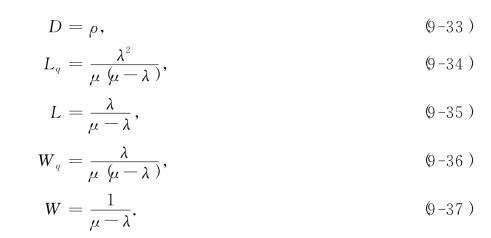
可以证明，若顾客在系统中的逗留时间为随机变量U，则

下面我们来计算M／M／1排队模型忙期Q的平均长度EQ.

对服务台来说，整个时间轴可以分成两部分：忙期与闲期.当一个顾客到达空着的服务台时忙期就开始，一直到服务台再一次变成空闲（就是说，系统中没有等待的顾客），忙期才结束.所谓闲期，就是指以服务台变成空闲开始到新的顾客到达为止这段时期.由最简单流性质可知，闲期长度遵从参数为λ的负指数分布，故闲期平均长度为.另一方面，P0＝1－ρ，因此在相当长的时期T0内，服务台空闲的时间总长度为T0（1－ρ），所以在T0时期内闲期的平均个数为T0（1－ρ）＝（1－ρ）λT0，它也等于T0内忙期的平均个数.又知T0时期内服务台忙碌时间总长度为T0ρ，因此忙期平均长度

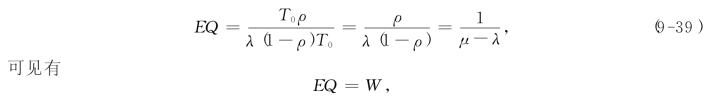
忙期的平均长度即为顾客在系统中逗留时间的期望值W.于是，一个忙期中所服务的顾客的平均数为

例9－8　为估计某邮局服务系统的效能，现以3分钟为一个时段，统计了100个时段中顾客到达的情况及对100位顾客的服务时间，有关数据列于表9－6和表9－7.设此服务系统为M／M／1排队模型.求系统有关的数量指标.

表9－6

表9－7

（续表）

解　先求出每时段内到达顾客的平均数

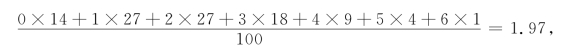
故顾客的平均到达率为

再计算每位顾客所需的平均服务时间，采用表9－5中时间区间的中值进行计算，可得：

所以此排队系统的服务率

于是，服务台服务强度为

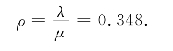
系统的空闲系数

顾客需要等待的概率

系统中平均队伍长度和平均等待队伍长度分别为

顾客平均逗留时间和平均等待时间分别为

服务台忙期的平均长度

例9－9　设某医生的私人诊所平均每隔20分钟有一位病人前来就诊，医生给每位病人诊断的时间平均需要15分钟.现设它为一个M／M／1排队模型.医生希望有足够的座位给来就诊的病人坐，使到达就诊的病人站着的概率不超过0.01.试问至少应为病人准备多少个座位（包括医生诊病时病人就座的一个座位）？

解　设k为需要的座位数.因而到达的病人站着的概率

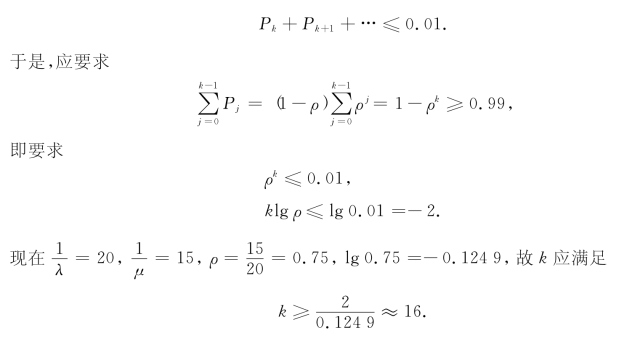(www.daowen.com)

即至少应为病人准备16个座位.

例9－10　设人们到售票口购买球赛票的平均到达率为每分钟1人，售票员卖一张票平均需20秒（到达间隔与服务时间都为负指数分布）.

（1）如果比赛开始前2分钟某球迷到达，若他买好票，估计他寻到其座位大约需1.5分钟，那么球迷能期望在球赛开始前坐好吗？

（2）该球迷在球赛开始前坐好的概率为多少？

（3）为了在球赛开始前坐好的把握为99%，该球迷应多早到达？

解　（1）本问题为M／M／1排队模型，如果以分钟为时间单位，则λ＝1，μ＝3，.于是，有

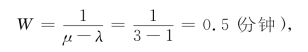
得到票的平均时间W与到达座位的时间之和恰为2分钟，所以球迷能期望在球赛开始前坐好.

（2）该问题即球迷在服务系统逗留时间U不超过半分钟的概率.有

（3）我们先求时间t，使P（U≤t）＝0.99.即要求

因此，该球迷能以99%的把握在2.3分钟内（等待和购票）得到一张票.因为在买到票以后他需要用1.5分钟找座位，所以该球迷必须提前2.3＋1.5＝3.8分钟到达，才能以0.99概率在球赛开始前就入座.

例9－11　若对于例9－3（取S＝3），如果对排队方式加以改变：在各个柜台前排成一个队列，且进入队列后不再变换，于是，得到3个M／M／1子系统.设每个队列的平均到达率

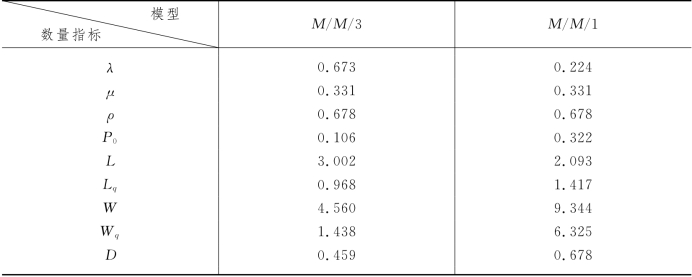
试将3个M／M／1排队模型与M／M／3排队模型作比较.

解　现按3个M／M／1排队模型计算有关数量指标，并与例9－3有关数据进行比较，得表9－8.从表9－8中各指标的对比可看出，单排队比3个队列有显著优越性.所以在安排排队方式时应加以注意.

表9－8

例9－12　表9－9给出了λ＝8，μ＝10的M／M／1和M／M／2模型以及服务率提高为μ＝20的M／M／1模型的有关数量指标，试讨论服务台的增减和服务率的增减对系统效能的影响.

表9－9

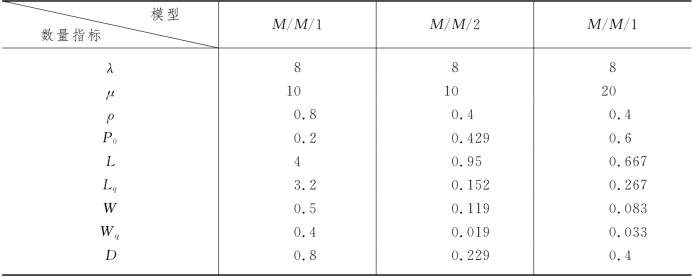
解　由表9－7可见，如果用增加服务速度的办法使服务能力增加一倍，则系统中的队长L由4减为0.667，顾客在系统中的逗留时间W由0.5减为0.083，为原值0.5的16.7%；如果采用增加一个服务台的方法提高服务质量，则系统中的队长L由4减为0.95，顾客在系统中的逗留时间W由0.5减为0.119，为原值0.5的23.8%.

比较这两种改进系统服务质量的方法（一种方法可以理解为采用大设备，提高μ，另一种方法可以理解为采用两台小设备，各台小设备的μ不变），可以明显看出，一台大设备的服务质量较好.尽管采用一台大设备时，等待队长Lq要比采用两台小设备时大一些，等待时间相应地要长些，但是可由服务速度较快来得到补偿，使系统中平均队长和顾客逗留时间比两台设备的相应值小.

例9－13　某工厂卸货台装卸设备的设计方案中，有3个方案可供选择，有关信息如表9－10所示.设货车按最简单流到达，平均每天（按10小时计算）到达15车，每车平均装货500袋.卸货时间服从负指数分布，每辆车在系统停留一小时的损失费为20元.试问该选择哪一个方案，使总费用最少？

表9－10

解　现在是对3个M／M／1模型进行选优，它们的平均到达率λ都一样：λ＝1.5（车／小时）.平均服务率依赖于方案，分别为：μ1＝＝2（车／小时），μ2＝＝4（车／小时），μ3＝＝12（车／小时）.一辆车在各系统平均逗留时间分别为

一辆车在系统逗留时间的平均损失费为20Wi，因为每天到达15辆车，所以每天到达的车辆在系统的平均逗留损失费为300Wi（i＝1，2，3），分别为600，120，28.5.

系统的利用率ρi＝（i＝1，2，3）分别为0.75，0.375，0.125.

系统每天的可变操作费用为ci，因此系统每天的实际操作费用为ciρi（i＝1，2，3），分别为

显然，有

每天总费用＝固定费用＋实际操作费用＋平均逗留损失费，

于是，我们得表9－11.可见，2＃方案费用最低，是3个方案中的最优方案.

表9－11

例9－14　若排队模型M／M／1的平均服务率μ可以调整，服务台提供服务的费用每单位时间为C1μ，顾客在系统中逗留单位时间的费用为C3，求最优服务率.

解　单位时间内系统总费用的期望值为