M/M/S排队模型为泊松输入、负指数分布服务、S个服务台、系统容量不受限制、顾客源数为无限的等待制排队模型,如图9-4所示.
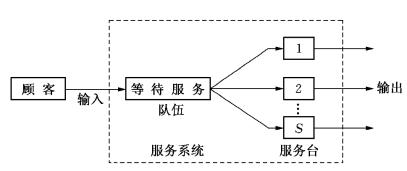
图9-4
假定到达率为λ的最简单流来到S个服务台的服务系统.一个顾客来到时,如果有一个以上的服务台空闲着,顾客就被随机地指派给任何一个有空的服务台进行服务;若所有服务台均在服务,则顾客排成一个队伍等待服务,顾客服务时间与顾客到达间隔时间相互独立,遵从参数为μ的负指数分布.
设ξ(t)为系统在时刻t时的队长,它是一个随机变量.若ξ(t)=j≤S,表示在时刻t有j个服务台正在进行服务,而剩下的S-j个服务台空闲着;若j>S,则表示在时刻t所有的S个服务台均在进行服务,且有j-S个顾客正在排队等待.可以证明{ξ(t)|t≥0}是一个生灭过程,其状态集I={0,1,2,…}.
由于顾客到达间隔T和顾客服务时间V分别服从参数为λ和μ的负指数分布,由式(9-14)和式(9-15)知,当t>0,对充分小的Δt,有
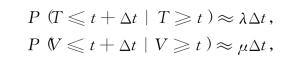
换言之,在Δt时间内来一个顾客的概率为λΔt+o(Δt);在Δt时间内一个服务台服务完一个顾客的概率为μΔt+o(Δt).于是,若j个服务台都在服务,那么j个服务台服务完一个顾客的概率为
![]()
我们有状态转移图(见图9-5).可见,对该生灭过程来说,有λj=λ,j=0,1,2,…,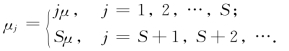
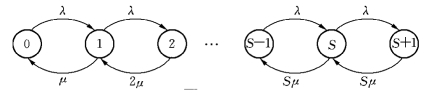
图9-5
正如我们在前面已指出过的,我们关心的问题是此生灭过程的稳态概率.我们来考虑定理9-3的条件式(9-4).易知有
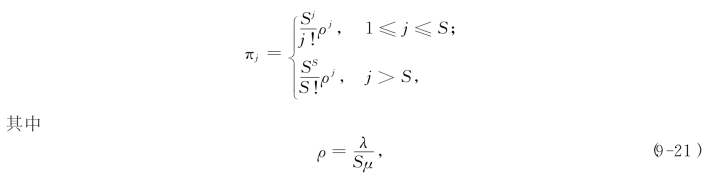
我们称ρ为服务强度,表示每个服务台在单位时间内的平均负荷,也即每个服务台的利用率.
可知,当ρ<1时,式(9-4)成立:
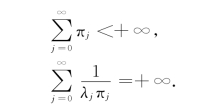
因此,在ρ<1条件下,根据定理9-3便得系统队长的稳态概率:
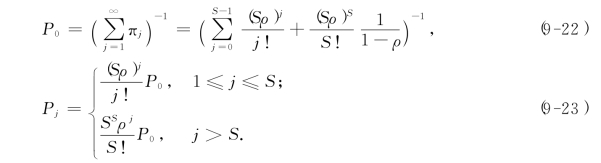
显然,P0即该系统的空闲系数.
所有服务台均被占用,以致来到一个顾客需要等待的概率D为

若S较小时,也可采用下式来计算D:

根据L和Lq定义,可得:
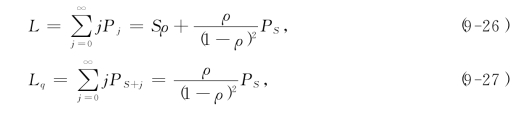
设Uq为顾客的等待时间,则该随机变量的分布函数为
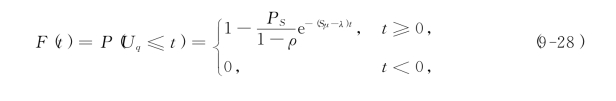
特别
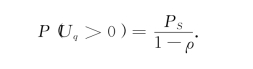
它与等待概率的表达式相同,这是很自然的.
又可知
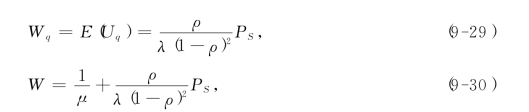
对于ρ≥1的系统,可知Pj=0对一切j成立,这表示如果将这一系统维持一段很长的时间,系统中的顾客队伍就会无限长.
例9-3 某超级市场,顾客从货架上挑选各类商品,出门前到柜台前付款.现有两个收款柜台,若都不空闲,顾客就排成一队,否则,顾客可在任一个柜台付款.设此服务系统是M/M/2排队模型.为了估计该系统的效能,现在柜台前作了如下统计:以两分钟作为一个时段,依次记下各个时段里来到的顾客数,并记下了这些顾客在柜台旁付款所花费的时间.下面给出有关数据:
(1)顾客来到数:在相继的26个时段里依次来到付款柜台前的顾客数为:1 3 0 1 0 0 1 1 2 1 0 1 3 2 5 1 2 2 1 0 0 1 0 3 3 1;
(2)付款时间(分:秒):4:35,3:02,5:27,4:33,2:35,1:45,0:15,3:45,0:15,4:20,2:39,4:51,5:45,0:23,2:30,3:26,1:48,1:16,1:24,4:17,3:07,1:40,5:53,2:31,3:28,0:54,0:38,6:55,1:33,6:20,0:59,2:03,1:29,5:24,3:50.
试估计该系统的效能.
解 由已知数据可知每时段(2分钟)平均到来顾客![]() =1.346,从而,该最简单流的参数(https://www.daowen.com)
=1.346,从而,该最简单流的参数(https://www.daowen.com)
![]()
顾客的平均服务时间
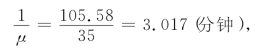
于是,该负指数分布的参数
![]()
本问题为M/M/2排队模型,所以
![]()
它表明这一系统运营一段时间后,系统中的顾客队伍长度会趋于无穷大.
为了使这系统能趋于稳定,现增设一个付款柜台,于是,问题成为M/M/3排队模型,因此有

柜台的利用率为0.678,系统的空闲系数为0.106.
例9-4 平均每小时有6列货车到达某货站,服务率为每小时2列,问要多少站台才能使货车等待卸车的概率不大于0.05?设该系统为M/M/S排队模型.
解 现系统为M/M/S,λ=6,μ=2,要使ρ=![]() <1,可见站台数不能少于4.
<1,可见站台数不能少于4.
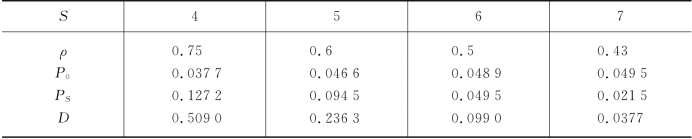
我们对S=4,5,6和7分别求出相应的ρ,P0,PS和D,如表9-3所示.可见,应设置7个站台.
表9-3
下面我们来讨论M/M/S排队系统的静态优化问题——系统设计的最优化.
我们建立系统的有关费用模型(考虑在单位时间内使服务费用和顾客等待(或逗留)费用之和最小),然后对有关的参数的优化进行决策.
服务费用是与服务水平(例如:代表服务机构能力的平均服务率,设备条件如服务台个数、系统容量)密切相关的,一般说来,它是可以确切计算或估计的,而顾客的等待费用对大部分排队模型就很难估算.
例9-5 若M/M/S排队系统的服务台个数可以调整,每个服务台在单位时间内的服务费用为C1(无论服务与否),顾客等待一个单位时间的费用为C2,求使总费用最低的最佳服务台个数.
解 等待队长是在变化的,而等待队长的期望值为Lq,因此,在单位时间内总费用期望值为

例9-6 一个服务台经营费用每小时15元,顾客等待单位时间费用50元,顾客到达为最简单流,每小时16个顾客,服务时间为负指数分布,服务率为每小时4个顾客,求单位时间总费用最低的服务台个数.
解 现在λ=16,μ=4,于是ρ=![]() .为满足条件ρ<1,应有S≥5.又
.为满足条件ρ<1,应有S≥5.又
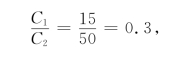
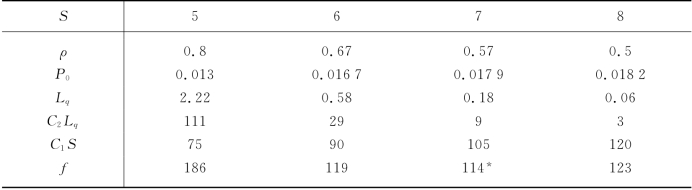
我们用边际分析法来求S*,计算过程见表9-4.
表9-4

由于0.3∈[0.12,0.4],因此最优解S*=7.
如果我们采用枚举法,则得表9-5.所以,最佳服务台个数为7,单位时间最低费用为114元.
表9-5
例9-7 对于M/M/S模型,若顾客在系统逗留一个单位时间的费用为C3,每个服务台在单位时间的服务费用为C1,求使总费用最低的最佳服务台个数.
解 单位时间总费用的期望值
![]()
类似于例9-5,最佳服务台个数S*应满足下列不等式:
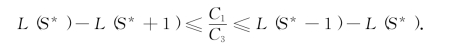
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







