【摘要】:爱尔朗分布的密度函数为其中参数μ>0,k称为阶数.若顾客服务时间V服从爱尔朗分布,则V的数学期望和方差分别为可以证明,如果ξ1,ξ2,…
爱尔朗(Erlang)分布的密度函数为
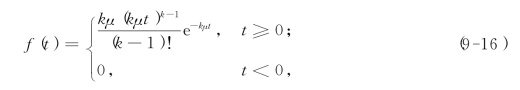
其中参数μ>0,k称为阶数.
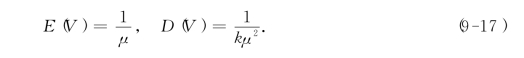
可以证明,如果ξ1,ξ2,…,ξk是k个相互独立的随机变量,且服从同一参数kμ(μ>0)的负指数分布,则随机变量
![]()
服从k阶爱尔朗分布.(www.daowen.com)
例如,如果顾客要连续接受串联的k个服务台的服务,各服务台服务时间相互独立,且服从相同的负指数分布(参数kμ>0),那么顾客被这k个服务台服务完所需的总时间就服从爱尔朗分布(当然,对顾客连续服务时,这里假设:必须在所有k个服务台完成对某一顾客的服务后,下一个顾客才能进入第一个服务台).
由于负指数分布的特性说明顾客服务时间短的可能性比服务时间长的可能性大,所以,在实际应用中负指数分布受到一定的限制,而爱尔朗分布却具有较大的适应性.
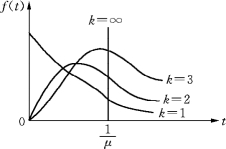
图9-2
图9-2给出n个不同k值的爱尔朗分布的密度函数.
事实上,当k=1时,爱尔朗分布即为负指数分布;当k增大时,爱尔朗分布的图形逐渐变为对称的;当k≥30时,爱尔朗分布近似于正态分布;当k→+∞时,由式(9-17)可知D(V)→0,因此,这时爱尔朗分布化为确定型分布(参看图9-2).所以k阶爱尔朗分布可看成完全随机型与完全确定型之间的中间型,能对现实世界提供更为广泛的适应性.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关运筹学方法与模型 第2版的文章








