若用N(t)表示在[0,t)时间内到达某服务系统的顾客数,则对于每个给定的时刻t,N(t)都是一个随机变量.我们称依赖于连续参数时间t的随机变量族{N(t)|t∈[0,A)}为一个随机过程.称N(t)的值为在时刻t时过程所处的状态,N(t)取值的全体称为状态集,记作I,I={0,1,2,…}.
假设对于任意的t1<t2<…<tn<tn+1,有

则称随机过程{N(t)|t∈[0,A)}为马尔柯夫(Markov)过程.式(9-1)所表示的性质称为“马尔柯夫性”或“无后效性”.它的实际背景就是说:如果以tn表示现在时刻,tn+1表示未来时刻,t1,…,tn-1表示过去的一系列时刻,则顾客到来的过程在tn以前所处的状态,对预言过程在tn以后的状态不起直接的作用.或者说,在已知“现在”的条件下,“将来”与“过去”是独立的.
下面我们着重介绍马尔柯夫过程之一——泊松(Poisson)过程.
若状态集I={0,1,2,…}的随机过程{N(t)|t∈[0,A)}具有所谓的独立增量性:对任一组t1<t2<…<tn(n≥3),随机变量
![]()
相互独立.同时,对任意t∈[0,A),有
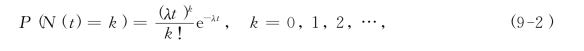
其中参数λ>0,则称这个过程为泊松过程.
独立增量性说明在互不相交的时间区间[t1,t2),[t2,t3),…,[tn,tn-1)内顾客来到系统的情况是相互独立的.不难验证,“独立增量性”这个条件比“马尔柯夫性”来得强.
由概率论有关知识知道,
![]()
它为在时间区间[0,t)内到达的顾客的平均数.从而,λ即为单位时间间隔内到达顾客的平均数.
在排队论里,人们常把泊松过程称为最简单流,参数λ称为最简单流的强度.在具体的实际问题中,λ是不难由统计资料求得的.
下面我们给出使泊松过程得以实现的比较广泛的条件.

我们现在对上述定理中的3个条件给出直观上的解释:
由独立增量性可知,在[0,A)中的区间[s,s+t)内来到k个顾客这一事件与区间[0,s)内来到的顾客的情况相互独立.换言之,对在[0,s)内顾客来到的情况所作的任何假定下,计算出来的在[s,s+t)内来到k个顾客的条件概率都相等.过程具有独立增量性,必然具有马尔柯夫性.
平稳性说明在[s,s+t)内来到的顾客数只与区间的长度t有关而与起点s无关.换言之,过程的统计规律不随时间的推移而改变,在同样长度的时间间隔内来到k个顾客的概率是一个常数.
普通性表明,在同一瞬时到达两个或两个以上顾客实际上是不可能的,换言之,在充分小的时间间隔中,最多到达一个顾客.
泊松过程在排队论中的地位与正态分布在概率论中的地位相同.但是,我们需要指出,独立增量性、平稳性和普通性在实践中并不是经常能够满足的.例如平稳性对电话呼唤流就显然不成立,白天的呼唤就比晚上多.虽然如此,最简单流仍然可以认为是实际现象相当程度上的近似,特别如巴尔姆辛钦(Palm-Xинчин)极限定理断言:大量相互独立小强度的随机流之和近似于一个最简单流,只要每个加项流都是平稳与普通,同时满足一些足够普通的条件.
概率论的中心极限定理告诉我们:足够多的独立随机变量之和近似于正态分布,而不管这些随机变量是什么分布.
而巴尔姆-辛钦极限定理正如中心极限定理一样,向我们阐明了为什么最简单流正如正态分布那样,经常会在实际生活中出现.
例如,到达电话局的总呼唤流是个别用户(强度相对地很小)发出电话呼唤的总和,而每一个别用户的呼唤可近似地看成平稳普通的流,且它们之间相互独立,因此,到达电话局的呼唤流就近似地视为最简单流.
正由于最简单流这种足够接近实际的性质,以及其简单而易于处理,因而在排队论中把它作为研究实际问题的一个起点.
例9-1 某天上午,从10:30到11:47,每隔20秒钟统计一次来到某火车站售票处的旅客数,共得230个记录.整理后得到如表9-2所示的统计结果.试用一个泊松过程来描述售票处的旅客的到达过程.
表9-2(https://www.daowen.com)

解 要描述这个到达过程只要求出参数λ即可.根据λ的意义,我们先求出每20秒钟内到达售票处的旅客的平均数
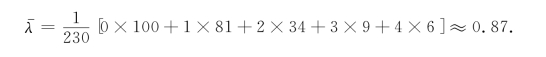
于是,每分钟平均到达的旅客数为
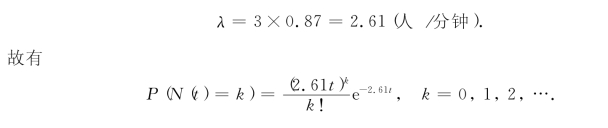
对于描述顾客到达情况的随机过程{N(t)|t∈[0,T)},我们也可以用随机变量序列
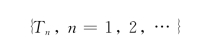
来描述,其中
![]()
为第n位顾客到达时刻tn与第n-1位顾客到达时刻tn-1之间的时间间隔(设t0=0).
对于泊松过程,我们有如下定理.
定理9-2 顾客到达过程{N(t)|t∈[0,A)}是一个参数为λ的泊松过程的充分必要条件为:相应的顾客到达间隔Tn(n=1,2,…)是一族相互独立同分布的随机变量,它们的分布函数为负指数分布:
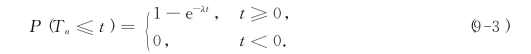
由此定理可知,“顾客流是最简单流”与“顾客到达间隔相互独立且服从相同的负指数分布”是等价的两种描述方式.
由于负指数分布的数学期望
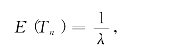
所以对于最简单流,顾客到达时间间隔的平均长度为![]() .
.
例9-2 在某个交叉路口观察了25辆向北行驶的汽车到达路口的时刻,其记录如下(开始观察时刻为0,单位为秒):
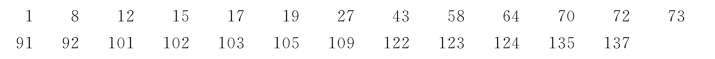
试用一个泊松过程来描述该到达过程.
解 该车流是一个最简单流,因此汽车相继到达的时间间隔Tn,n=1,2,…相互独立,服从同一分布——负指数分布.现在估计负指数分布的参数λ.
汽车相继到达路口的时间间隔为

所以,服从如下分布的独立同分布随机变量族{Tn,n=1,2,…}描述了该车流:
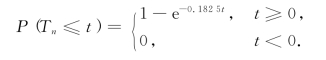
换言之,汽车到达路口的过程是一个以每秒来到0.182 5辆汽车的最简单流{N(t)|t≥0}:
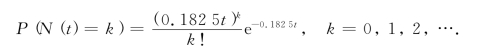
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







