这一节介绍若干个动态规划例题,目的在于通过这些例题使我们初步了解动态规划方法的计算细节和各类技巧.当然,要想得心应手地使用动态规划方法,仅仅掌握这几个例子的求解技巧还是远远不够的.
表8-9
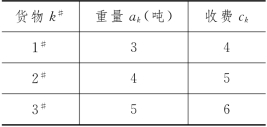
例8-3 (载货问题) 现有载重量为20吨的卡车,装用3种不同的货物.已知这3种货物的单件重量和装载收费如表8-9所示,又规定2#货物和3#货物都至多装两件.问如何装载这3种货物,可使该车一次运输的货物收费最多?
解 设xk为k#货物的装载件数.于是我们可得下列整数规划:

现在,我们应用动态规划方法来求解.我们把这个装载问题分成3个阶段,在第k阶段需要确定k#货物的装载件数.令
sk——对k#,…,3#货物允许的装载重量;
xk——k#货物的装载件数;
wk(sk,xk)——k#货物装载xk件时的收益:wk(sk,xk)=ckxk;
Tk(sk,xk)——sk+1=sk-akxk;
fk(sk)——对k#,…,3#货物允许载重sk时采取最佳决策所能获得的最大收益.递归方程为
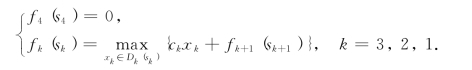
下面我们用逆序解法求解.
第一步,k=3,有方程
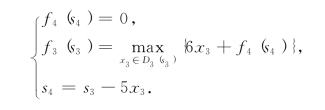
显然,S3={0,1,…,20},由于3#货物至多装载2件,因此,决策集合为
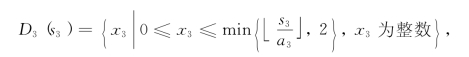
由表8-10给出.
表8-10

f3(s3)的计算过程如表8-11所示.
表8-11

第二步,k=2,有方程
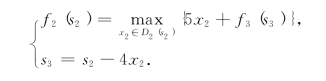
显然,s2={0,1,…,20}.由于2#货物至多装载2件,且a2=4,因此,决策集合为
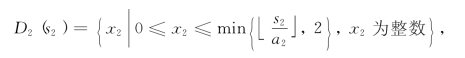
它由表8-12给出.
表8-12

在列举本阶段的可能状态时,我们希望将那些具有相同f2(s2)值的状态合并成一类,以减少计算次数.如果只孤立地考虑阶段2,则根据表8-12,我们将S2={0,1,…,20}划分成3个子集{0,1,2,3},{4,5,6,7}和{8,…,20}(我们称0,4和8为划分点),各个子集中的状态的决策集合相同,但是我们发现,同一个子集中的状态s2相应的f2(s2)值并不相同:例如s2=4和s2=5在同一个子集中,而表8-13告诉我们,f2(4)≠f2(5).所以,对S2的划分,要同时结合S3的划分来考虑.由表8-10和表8-12知:
表8-13

S3划分点向量(t1,t2,t3)=(0,a3,2a3)=(0,5,10),
S2划分点向量(u1,u2,u3)=(0,a2,2a2)=(0,4,8).
表8-14
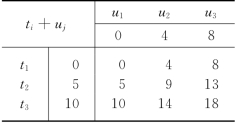
于是,我们计算S2关于f2(s2)的划分点ti+uj(i,j=1,2,3),如表8-14所示.因此,我们将S2={0,…,20}划分成9个子集:
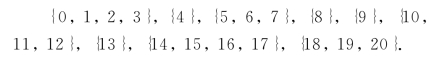
f2(s2)的计算过程由表8-15给出.
第三步,k=1,有方程
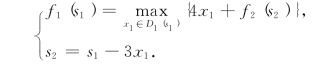
表8-15

显然,S1={20},D1(20)={0,1,…,6},f1(s1)的计算过程如表8-16所示.
表8-16

由顺序追踪法可知,本问题的最优策略为
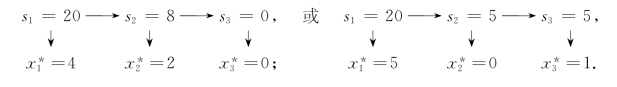
即最优装载方案有2个:
方案Ⅰ:1#货物装4件,2#货物装2件,3#货物不装;
方案Ⅱ:1#货物装5件,2#货物不装,3#货物装1件,装载收费26.
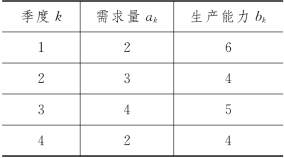
例8-4 (生产与存储问题) 某工厂安排明年4个季度某种产品的生产计划.市场对该厂该产品的需求量及工厂在各个季度的生产能力如表8-17所示.
每季度生产这种产品的固定成本F=3(与产品批量无关.不生产时则F=0),每件产品的成本c=1.本季度产品当季如不能出售,则需运到仓库存储,每季度每件产品的存储费g=0.5.每个季度仓库的最大库存量E=3.假设明年年初和年末的库存量均应为零,试问该厂应如何安排4个季度的生产,以保证在满足市场需求的前提下,使生产和存储的总费用最小?
表8-17
解 将每一个季度看作一个阶段,本问题就是一个4阶段的决策问题.令
sk——第k季度初的仓库库存量;
xk——第k季度的生产量;
wk(sk,xk)——第k季度的生产和存储费:
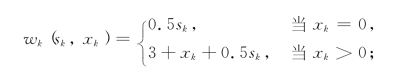
Tk(sk,xk)——sk+1=sk+xk-ak;
fk(sk)——在第k季度初库存量为sk的条件下,为满足市场需求,从第k季度至年末生产和存储该产品的最低费用.
递归方程为
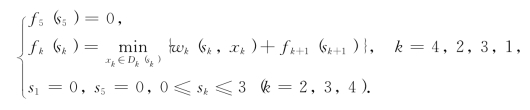
现在我们用逆序解法求解.
第一步,k=4,有方程
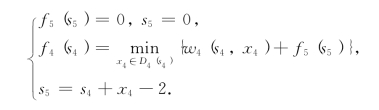
因为s5=0,所以x4=2-s4.由于x4≥0,所以有0≤s4≤2,S4={0,1,2}.计算过程如表8-18所示.
表8-18

第二步,k=3,有方程
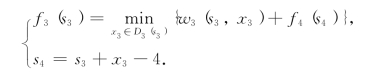
因为0≤s4≤2,所以有4≤s3+x3≤6.又根据问题假设条件0≤s3≤E=3,0≤x3≤b3=5,因此S3={0,1,2,3},决策集合D3(s3)由表8-19给出.计算过程如表8-20所示.
表8-19

表8-20

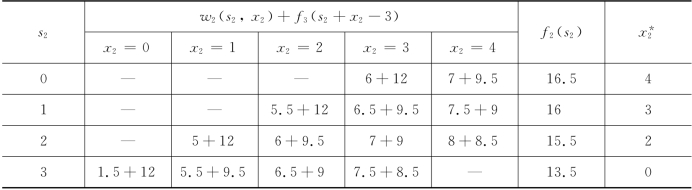
第三步,k=2,有方程
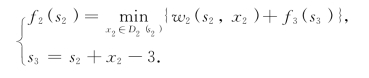
因为0≤s3≤3,所以有3≤s2+x2≤6.根据题设0≤s2≤E=3,0≤x2≤b2=4,因此S2={0,1,2,3},决策集合D2(s2)由表8-21给出.计算过程如表8-22所示.
表8-21

表8-22
第四步,k=1,有方程
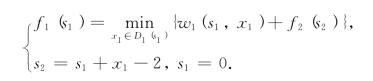
显然,s2=x1-2,据题设0≤s2≤E=3,所以有0≤x1-2≤3,即2≤x1≤5.因此D1(0)={2,3,4,5}.计算过程如表8-23所示.
表8-23
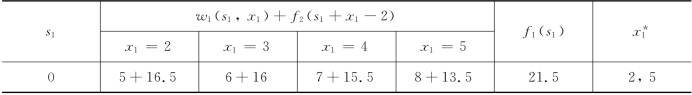
由顺序追踪法可知本问题的最优策略为
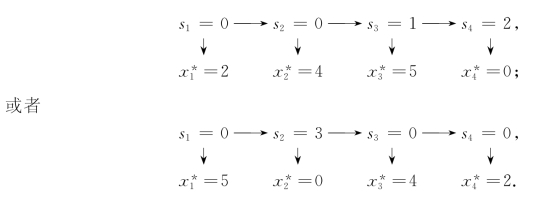
即最优生产方案有2个:
方案Ⅰ:4个季度生产的产品件数分别为
![]()
方案Ⅱ:4个季度生产的产品件数分别为
![]()
总的费用为21.5.
例8-5 (仪器置换问题) 某科学实验可用1#,2#,3#不同仪器中的任一套去完成.每做完一次试验后,如果下次仍用原来的仪器,则需对该仪器进行检查整修而中断试验;如果下次换用另外一套仪器,则需拆装仪器,也要中断试验.假定一次试验时间比任何一套仪器的整修时间都长,因此一套仪器换下来隔一次再重新使用时,不会由于整修而影响试验.设i#仪器换成j#仪器所需中断试验的时间tij如表8-24所示.现要做4次试验,问应如何安排使用仪器的顺序,使总的中断试验的时间最小?
表8-24
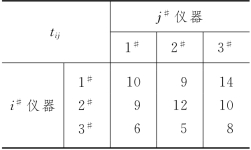
解 假设每次中断试验为一个阶段,则本问题为3阶段的决策过程.令sk——第k次中断试验前所使用的仪器;
xk——第k次中断试验而恢复试验时采用的仪器;
wk(sk,xk)——第k次中断试验所需时间:wk(sk,tk)=![]() ;
;
Tk(sk,xk)——sk+1=xk;
fk(sk)——当第k次中断试验前使用仪器为sk时,从第k次中断试验直至做完第4次试验所花费的最短中断时间.
递归方程为
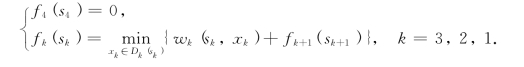
显然,第k阶段的状态集合Sk和决策集合Dk(sk)都为{1,2,3}(k=1,2,3).
现在我们用逆序解法来求解.
第一步,k=3,有方程
![]()
计算过程如表8-25所示.
表8-25

第二步,k=2,有方程
![]()
计算过程如表8-26所示.
表8-26

第三步,k=1,有方程
![]()
计算过程如表8-27所示.
表8-27



表8-28

表8-29
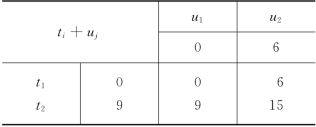
我们将S3={0,…,24}划分成4个子集:{0,…,5},{6,…,8},{9,…,14}和{15,…,24}.
f3(s3)的计算过程如表8-30所示.
表8-30

第三步,对k=2,有方程
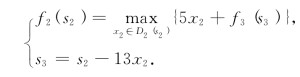 (https://www.daowen.com)
(https://www.daowen.com)
显然,S2={0,…,24}的划分点为v1=0,v2=13.对于s2∈{0,…,12},有D2(s2)={0}.
对于s2∈{13,…,24},有D2(s2)={0,1}.
由第二步知,S3关于f3的划分点qj(j=1,2,3,4)分别为0,6,9,15.于是,为计算vi+qj,我们列出表8-31,由该表可知,S2关于f2(s2)的划分点分别为0,6,9,13,15,19,22(由于v2+q4=13+15=28>24,故v2+q4=28不作为划分点).
表8-31

f2(s2)的计算过程如表8-32所示.
表8-32
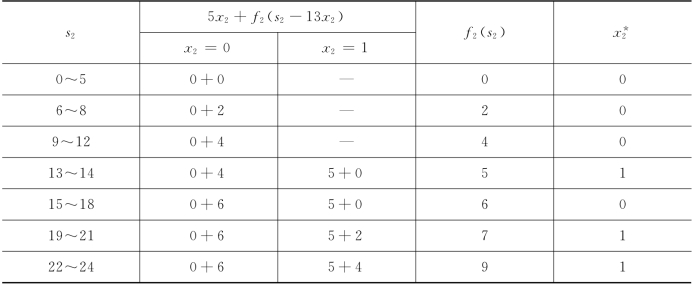
第四步,对k=1,有方程
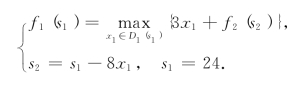
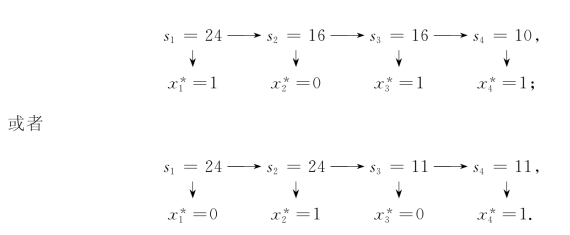
显然,D1(s1)={0,1}.f1(s1)的计算过程如表8-33所示.于是,根据顺序追踪法可知,0-1背包问题有2个最优解![]() ,最优值f*=9:
,最优值f*=9:
表8-33

例8-7 (可靠性问题) 某种仪表由3种不同的元件串联而成,任一个元件的故障将造成整台仪表的故障.每种元件又都有3种规格,设k#元件j#规格的可靠性为Rkj,所需费用为Ckj.生产每台仪表的费用限额E为10.试问如何选用各种元件的规格,使得仪表的可靠性最大?Rkj及Ckj分别由表8-34和表8-35给出.
表8-34
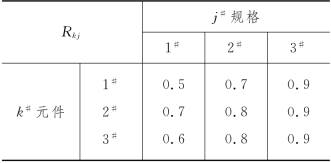
表8-35
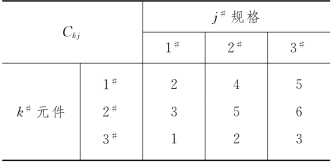
解 我们把这个问题分成3个阶段.在第k阶段要确定k#元件的规格.对本问题我们采用顺序解法来解.令
sk——仪表上配备1#,…,k#元件时允许使用的费用;
xk——k#元件所选用的规格;
wk(sk,xk)——k#元件采用规格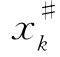 时的可靠性,有
时的可靠性,有
![]()
Tk(sk,xk)——sk-1=sk-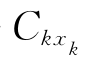 ;
;
fk(sk)——在费用限额为sk的条件下,1#,…,k#元件串联时相应部分可获得的最大可靠性.递归方程为
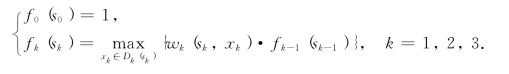
下面我们用顺序解法求解.
第一步,对k=1,有方程
![]()
由于仪表是由3种元件串联而成,每一种元件都不可缺少,而由表8-35知,配备k#元件的最小费用为Ck1,因此s1应满足条件
![]()
即状态集合S1={2,3,4,5,6}.而决策集合D1(s1)由下式给出:
![]()
由此,我们得表8-36.
表8-36

f1(s1)的计算过程如表8-37所示.
表8-37
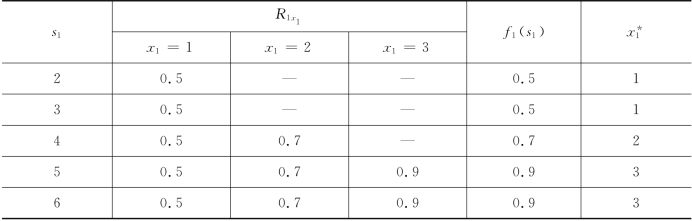
第二步,对k=2,有方程
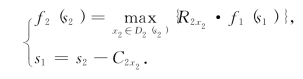
同k=1时对状态s1的讨论一样,s2应满足条件:
![]()
即有S2={5,…,9}.由于2=C11≤s1=s2-C2x2,所以,决策集合D2(s2)由下式给出:
![]()
我们即可得表8-38.f2(s2)的计算过程如表8-39给出.
表8-38

表8-39
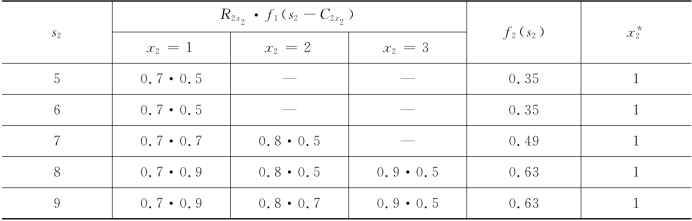
第三步,对k=3,有方程
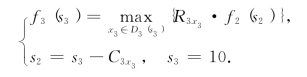
现在S3={10}.由于5≤s2=10-C3x3,因此,有
![]()
f3(s3)的计算由表8-40给出.
表8-40

此时,运用逆序追踪法,由状态转移方程可知最优策略为
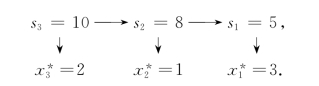
因此,最佳设计方案为:1#元件选3#规格,2#元件选1#规格,3#元件选2#规格.此时,仪表的可靠性为0.504.
例8-8 (生产计划问题) 用动态规划方法求解第一章例1-20(假设每季度对产品的需求量和生产能力都是10的倍数).
解 将每一个季度看作一个阶段,本问题就是一个4阶段的决策过程.令
sk——第k季度初的库存量;
xk——第k季度的产量;
wk(sk,xk)——第k季度的生产成本和存储费之和:wk(sk,xk)=0.2sk+dkxk;
Tk(sk,xk)——sk+1=sk+xk-bk;
fk(sk)——当k季度初的库存量为sk时,从第k季度到年末,厂方为完成合同所需支付的最少的生产费用.递归方程为
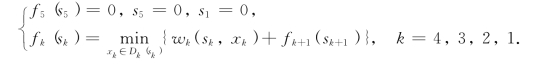
下面用逆序解法求解.
第一步,对k=4,有方程
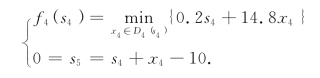
由于前3个季度至多生产
![]()
而前3个季度合同的需求量
![]()
所以,s4≤90-70=20.又x4=10-s4,0≤x4≤a4=10,从而0≤s4≤10,S4={0,10}.当s4=0时,D4(0)={10};当s4=10时,D4(10)={0}.f4(s4)的值由表8-41给出.
第二步,对k=3,有方程
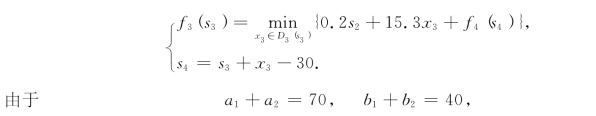
因此s3≤30.据题设30-s3≤x3≤20,因此有s3≥10.故状态集合S3={10,20,30}.决策集合由表8-42给出.
表8-41

表8-42

在表8-42中,当s3=30时,因为s4≤10,而s4=s3+x3-30,所以x3≤10.
f3(s3)的计算过程如表8-43所示.
表8-43

第三步,k=2,有方程
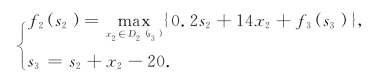
因为a1=30,b1=20,所以s2≤10.又因为a2+a3+a4=70>b2+b3+b4=60,所以允许s2=0.从而,状态集合S2={0,10}.
由于10≤s3≤30,s3=s2+x2-20,因此有30-s2≤x2≤50-s2,又考虑到x2≤a2=40,于是对s2=0或10来说,应有
表8-44

![]()
决策集合D2(s2)由表8-44给出.f2(s2)的计算由表8-45给出.
表8-45

第四步,对k=1,有方程
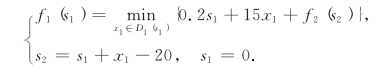
由于s1=0,故根据题设应有
![]()
即S1={0},D1(0)={20,30}.
表8-46给出了f1(s1)的计算.
表8-46

用顺序追踪法即得本问题的最优策略:
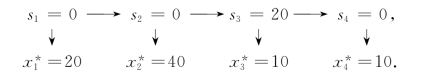
即明年的最优生产计划为各季度分别生产20,40,10和10(吨),总费用为1 165万元.
在上述求解过程中,我们可以发现,在第k阶段,无论sk取Sk中何值,wk(sk,xk)+fk+1(sk+1)或随xk增大而增大(如k=3,1),或随xk的增大而减少(如k=2),如果进一步经过变换(见下面分析),可知wk(sk,xk)+fk+1(sk+1)是xk的线性函数,这使我们想到,如果把xk和sk视作连续型变量,是否可以利用微积分中的方法,来求fk(sk)及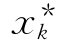 ?下面我们来探索这一方法.
?下面我们来探索这一方法.
第一步,对k=4,有
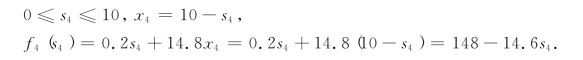
第二步,对k=3,有
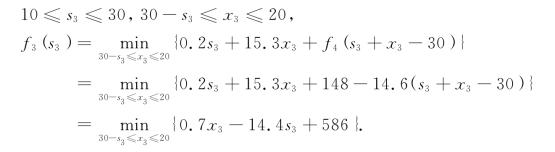

例8-9 (机器负荷问题) 设某种机器可以在高、低两种不同的负荷下进行生产.若年初有x台机器在高负荷下进行生产,则产品年产量a=8x,机器的年折损率β=0.3;若年初有y台机器在低负荷下进行生产,则产品年产量b=5y,机器的年折损率α=0.1.若初始时有性能正常的机器1 000台,要求制定机器负荷的4年分配计划:每年年初分配正常机器在不同负荷下工作的台数,使4年内产品总产量最大.
解 这是一个4阶段决策过程,阶段k表示第k年度.令
sk——第k年度初正常机器台数;
xk——第k年度初分配在高负荷下工作的机器台数;
wk(sk,xk)——sk台机器在第k年的产品产量:
![]()


即4年内机器负荷分配的最佳方案为:第一年年初把全部正常机器投入低负荷生产,后3年每年年初把正常机器投入高负荷生产,4年内产品的最高产量f1(1 000)=20 718.
例8-10 (生产计划问题) 工厂在3个季度中安排某种产品的生产计划.若该季度生产此种产品x(吨),则成本为x2.当季生产的产品未销售掉,则进库后,季末需付存储费,每吨产品每季的存储费为1.现估计3个季度对该产品的需求量ak分别为100(吨),110(吨)和120(吨),又设第一季度初及第三季度末库存量为零.假设各季度产品的生产量不受限制,试问如何安排3个季度的生产计划,使产品的生产成本和存储费之总和最低?
解 本问题为一个3阶段的决策问题,现用顺序解法求解.令
sk——第k季度末的库存量;
xk——第k季度的产品生产量;
wk(sk,xk)——第k季度的生产成本和存储费之和:wk(sk,xk)=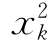 +sk;
+sk;
Tk(sk,xk)——sk-1=sk+ak-xk;
fk(sk)——第k季度末库存量为sk时,从第一季度至第k季度的最低生产费用.递归方程为
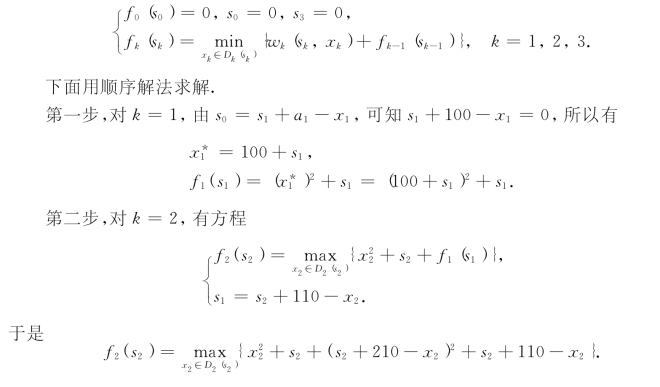





免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







