现在我们在上一节引例的基础上引入动态规划的一些基本概念并给出一般模式.

（1）阶段.如果一个问题确定能用动态规划方法求解时，那么必须恰当地把问题的过程划分为若干个相互联系的阶段.通常根据时间和空间的自然特征来划分阶段.阶段的编号采取顺序编号，阶段的个数N称为历程.例如对于例8－1最短路径问题来说，N＝4.

历程N可以是确定的，也可以是不确定的.在本章研究的问题中，N都是确定且有限的.

（2）状态.第k阶段的状态是指过程在该阶段所处的各种可能情况.它为问题的某种特征.描述过程在第k阶段状态的变量，称为状态变量，用sk表示.sk通常以一个数或一个向量（多维情形）来描述.sk取值的全体记作Sk，称作第k阶段的状态集合.

状态的定义在动态规划中往往是最重要的概念.它必须具备3个特性：

①描述性.各阶段状态的演变能描述决策过程.例如最短路径问题引例中，状态的演变A→B3→C3→D1→E描述了整个决策过程.

②无后效性.如果第k阶段的状态给定，则在这阶段以后过程的发展不受这阶段以前各个阶段状态的影响.也就是说，过程未来的发展，只与过程的现在状态有关，而与过程的过去状态无关.

例如，在最短路径问题引例中，若旅行者在第3阶段处在状态s3＝C3，以后的问题就只是旅行者如何从C3出发走到E，至于第1、第2阶段所处状态（即旅行者从起点A如何走到C3），对以后各阶段旅行者如何选择到达点已无直接的影响.

在对实际问题建立动态规划模型时，如果状态的规定方式不能满足无后效性，这时，就必须改变状态的定义而使之满足无后效性.

③可知性.各阶段状态变量的取值，直接或间接是可知的，也就是说，第k阶段的状态集合Sk是给定的.

可以说，过程在第k阶段的状态概括了对本阶段及以后各阶段作出一个可行决策所需要的全部信息.

（3）决策.当第k阶段的状态sk给定后，从该状态演变为第k＋1阶段状态时所作的选择称为决策.描述决策的变量称为决策变量，用xk（sk）表示，简记为xk.xk通常用一个数或一个向量来描述.xk（sk）取值的全体记为Dk（sk），称为第k阶段的决策集合，sk取值不同，相应的决策集合也可能不同.

状态变量sk与决策变量xk可为离散型变量，也可为连续型变量.

（4）策略.由过程的第1阶段初始状态s1开始，逐阶段演变至终止状态sN＋1的过程称为问题的全过程.由每阶段的决策xk（sk）（k＝1，…，N）组成的序列｛x1（s1），x2（s2），…，xN（sN）｝称为策略.

由第k阶段状态sk开始逐阶段演变至终止状态sN＋1的过程称为k～N子过程，其决策序列｛xk（sk），xk＋1（sk＋1），…，xN（sN）｝称为子策略.

全体策略称为策略集合.策略集合中使目标实现最优的策略，称为最优策略.

（5）状态转移方程.第k＋1阶段的状态sk＋1与第k阶段的状态sk、决策xk之间有函数关系

并称其为状态转移方程.

（6）权函数.在第k阶段，当状态取定sk、决策取定xk时，该阶段所实现的效益指标（例如距离、时耗、利润、成本等）称为权函数，以wk（sk，xk）表示之.

wk（sk，xk）不一定有解析式.

（7）指标函数.若第k阶段的状态为sk，当采用了最优子策略后，从阶段k到阶段N可获得的效益，称为指标函数，记为fk（sk）.实现fk（sk）值的xk记为.

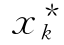若第k阶段状态为sk，本阶段决策为xk（于是第k＋1阶段状态为sk＋1），从第k＋1阶段开始采用最优子策略则第k阶段至第N阶段可获得的效益函数为

其中，符号⊙表示加法或乘法运算.我们称此含义下的效益函数具有可加性或可乘性，即该效益函数为可分函数.

（8）递归方程.称下列方程为递归方程：

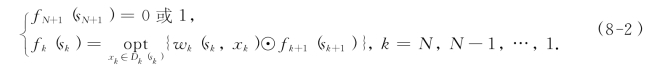
其中，符号opt视问题性质可取min或max，同时，当符号⊙取加法运算时，取fN＋1（sN＋1）＝0；当符号⊙取乘法运算时，取fN＋1（sN＋1）＝1.

动态规划递归方程的建立，是基于下述动态规划的最优化原理（R·贝尔曼（R.Bellman）提出）：

作为整个过程的最优策略具有这样的性质：无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略.简言之，最优策略的子策略，构成最优子策略.

根据最优化原理建立的递归方程，把原问题嵌入到一族相互联系的同类型的子问题中，使求解变得可能和容易.

由于用递归方程（8－2）和状态转移方程（8－1）求解动态规划的过程，是由第N阶段向前递归至第1阶段，故这种方法称为逆序解法.

综上所述，如果一个问题能用动态规划方法求解，那么，我们可以按下列步骤建立动态规划的数学模型：

①划分阶段，并正确地定义各阶段状态变量使之具有描述性、无后效性和可知性3个特性，同时确定状态集合；

②定义决策变量，确定决策集合；

③确定权函数；

④建立状态转移方程；

⑤确定指标函数；

⑥建立递归方程.

由状态转移方程和递归方程，用逆序解法对动态规划模型求解，在求得f1（s1）和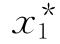（s1）后，则按下列方法寻找最优策略：

当s1仅取一个值时，由状态转移方程采用顺序追踪法来寻找最优策略：

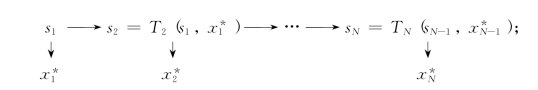
当s1可取一个以上值时，取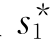满足：(www.daowen.com)

然后采用顺序追踪法来寻找最优策略：

例8－2　（投资问题）　现有资金5百万元，可对3个项目进行投资，投资额均为整数（单位为百万元）.假设2＃项目的投资不得超过3百万元，1＃和3＃项目的投资均不得超过4百万元，3＃项目至少要投资1百万元.投资5年后每个项目预计可获得的收益由表8－5给出.问如何投资可获得最大的收益.

表8－5

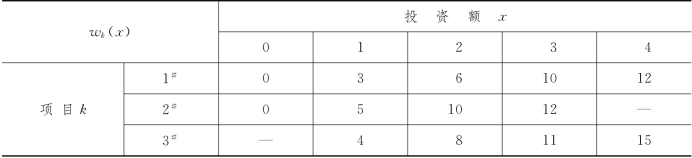
解　本问题是一个静态问题，但可以把它转化成动态问题：将这个投资问题分成3个阶段，在第k阶段要对项目k＃进行投资决策.令

sk——对k＃，…，3＃项目允许的投资额；

xk——对k＃项目的投资额；

wk（sk，xk）——对k＃项目投资xk后的收益：wk（sk，xk）＝wk（xk）；

Tk（sk，xk）——sk＋1＝sk－xk；

fk（sk）——当第k至第3项目允许的投资额为sk时所能获得的最大收益.

为了获得最大收益，必须将5百万元资金全部用于投资.故假想有第4阶段存在时，必有s4＝0.对于本问题，有下列递归方程：

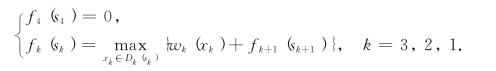
下面由状态转移方程和递归方程，用逆序解法求解.

第一步，k＝3，有方程

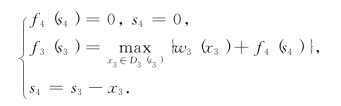
由于s4＝0，且3＃项目至少投资1百万元，至多投资4百万元，因此

计算过程如表8－6所示.

第二步，k＝2，有方程

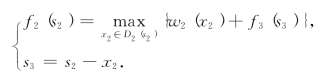
表8－6

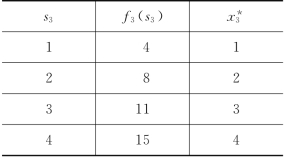
因为s3≥1，所以s2≥1，有S2＝｛1，…，5｝：当s2＝1，2，3，4时，D2（s2）＝｛0，…，s2－1｝；当s2＝5时，由于2＃项目至多投资3百万元，且s4＝0，因此，有D2（5）＝｛1，2，3｝.计算过程如表8－7所示.

表8－7

第三步，k＝1，有方程

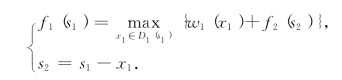
现在s1＝5，又1＃项目至多投资4百万元，因此有D1（5）＝｛0，1，2，3，4｝.计算过程如表8－8所示.

表8－8

由状态转移方程和顺序追踪法，得本问题的最优策略：

即最优投资方案有2个：

方案Ⅰ：1＃项目不投资，2＃项目投资2百万元，3＃项目投资3百万元.

方案Ⅱ：1＃项目投资1百万元，2＃项目投资2百万元，3＃项目投资2百万元.

最大收益均为21百万元.

在动态规划用逆序解法求解时，计算k～N子过程的方程利用了k＋1－N子过程的方程的计算信息，所以，一些非优的可行策略就被淘汰，在全体策略集合中，只明显地考虑一小部分可行的策略，因此说它也是一种隐式枚举法，它的计算量自然要比完全枚举法大大地减少.但是，动态规划方法只是解决多阶段决策过程的一个手段，而不是一种算法.不同的动态规划问题，递归方程的形式及复杂程度大不一样，同时，对k～N子过程的处理方法也不统一，需根据问题的各种特性来运用各类数学技巧.故而，判明一个实际问题能否建立动态规划模型以及对它怎样求解，需要我们相当的创造力及丰富的想象力.要培养这方面的能力，最好的途径是多多接触各种类型的动态规划的应用问题，研究这些问题的共同特征，通过知识的积累来提高构造动态规划模型的艺术技巧.动态规划方法的另一个不足之处是所谓“维数障碍”，当状态变量或决策变量是多维向量时，由于状态集合的庞大使可行的策略大大地增加，于是计算机的存储量及计算量都大大地增加，从而使得解状态维数很高的大型动态规划问题变得十分困难.

最后，我们还要指出，对某些动态规划问题，也可采用顺序解法求解，即递归方程的计算是从阶段k＝1开始，到阶段k＝N终止.此时，状态转移方程和递归方程分别是：

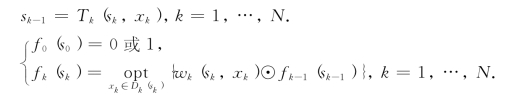
下一节我们将用具体的例题来说明当用顺序解法解时，如何建立动态规划模型.