例8－1　（最短路径问题）　一个旅行者由始点A出发，需经过4个阶段到达终点E.前面3个阶段分别有3个、4个和2个中转点，旅行者在每一阶段只能选择一个中转点作为本阶段的到达点，具体线路如图8－1所示，边旁参数为该边起点到终点的距离.求A至E的最短路径.

图8－1

对本问题我们可以用网络规划中的最短路径算法，求得图8－1中任一顶点至顶点E的最短路径及其长度，如图8－2所示（图中顶点旁括号中的数字为该顶点至E的最短路径长度）.

现在我们用动态规划方法来求A至E的最短路径及其长度，通过其求解过程来说明动态规划的基本思想并给出有关的术语.

若第k阶段旅行者的出发点记为sk，我们称sk为第k阶段的状态变量.第k阶段状态变量sk可取的顶点的全体记为Sk，我们称Sk为第k阶段的状态集合.例如在本问题中，S3＝｛C1，C2，C3，C4｝.状态变量取定某一个顶点，就说旅行者处于某个状态.

若第k阶段旅行者从状态sk出发，本阶段所选择的到达点记为xk（sk），我们称xk（sk）为决策变量，并简写为xk，xk依赖于sk.当sk选定，决策变量xk取点的全体记为Dk（sk），我们称Dk（sk）为决策集合.当状态变量sk取不同的点时，所得决策集合也可能不同.例如，取s2＝B1，有D2（B1）＝｛C1，C2｝；取s2＝B2，有D2（B2）＝｛C1，C2，C3，C4｝.

图8－2

显然，若第k阶段的状态变量sk及相应的决策变量xk（sk）一经确定，则第k＋1阶段的状态变量sk＋1也就完全确定.例如，第2阶段出发点s2取为B3，该阶段的到达点x2取为C3，则第3阶段的出发点s3也就确定，s3＝C3；因此，我们说sk＋1与sk，xk有函数关系，并以sk＋1＝Tk（sk，xk）表示之，通常称它为状态转移方程.在本问题中，显然，sk＋1＝xk.

第k阶段出发点sk至本阶段到达点xk的距离记为wk（sk，xk），我们称它为权函数.本问题的权函数由图8－1中边旁参数给出.

在网络规划这一章中我们已经介绍过最短路径的几何特征，它告诉我们，如果A至E的最短路径P在第k阶段以sk为出发点，则P中sk至终点E的子路P1，对于sk至终点E的所有可供选择的路线来说，必定也是最短路径，且路径P1及其长度与旅行者在sk以前所经历的路线无关.我们把这个几何特征称为这最短路径问题的最优化原理，并称状态sk具有无后效性.

动态规划方法解本问题的基本思想就是利用了最短路径问题的最优化原理：要求最短路径P，则先求子路P1，由P1往前逐阶段延伸，直至始点A.确切地说，如图8－2那样，先求出第4阶段状态变量s4（可取D1或D2）至E的最短路径，接着求第3阶段状态变量s3（可取C1，C2，C3或C4）至E的最短路径，再求第2阶段状态变量s2（可取B1，B2或B3）至E的最短路径，最后求得第1阶段状态s1（取A）至E的最短路径.

在递推过程中，求第k阶段sk至E的最短路径时，利用了第k＋1阶段sk＋1至E的最短路径的信息.

例如，假设第3阶段状态变量s3（可取C1，C2，C3或C4）至E的最短路径已求得，现在旅行者在第2阶段所处的状态s2为B1，他面临两个决策：x2（B1）＝C1或C2.如果此时旅行者选定本阶段的到达点为C1，那么，他在第3阶段所处的状态s3为C1，他以C1为出发点继续行走.由图8－2知，他必选C1至E的最短路径C1D1E（路径C1D2E比路径C1D1E长，因此被自动淘汰）.因为状态s3＝C1具有无后效性，所以路径B1C1D1E的长度＝w2（B1，C1）＋路径C1D1E的长度＝5＋5＝10；如果旅行者选本阶段的到达点为C2，那么，他在第3阶段以C2为出发点继续行走，由图8－2知，他必选C2至E的最短路径C2D2E，由状态s3＝C2的无后效性，路径B1C2D2E的长度＝w2（B1，C2）＋路径C2D2E的长度＝4＋8＝12.可见，旅行者在s2＝B1时的最佳决策（B1）＝C1，从而，由B1至E的最短路径为B1C1D1E，其长度为10.

若旅行者在第k阶段由状态sk出发至终点s5＝E的最短路径长度记为fk（sk），则由最短路径问题的最优化原理及状态的无后效性可知：

加上初始条件f5（s5）＝0（s5＝E），我们称它们为本问题的动态规划模型的递归方程.取得fk（sk）值的相应xk，我们记为.

由递归方程和状态转移方程，我们就可以求解本问题.下面我们采用表格形式逐步计算.

第一步，k＝4，有方程

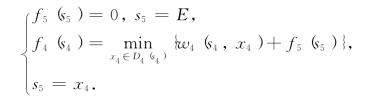
现在状态集合S4＝｛D1，D2｝，决策集合D4（s4）＝｛E｝，计算过程如表8－1所示.

表8－1(www.daowen.com)

第二步，k＝3，有方程

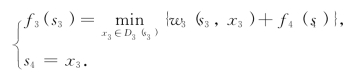
现在S3＝｛C1，C2，C3，C4｝，D3（Cj）＝｛D1，D2｝（j＝1，2，3），D3（C4）＝｛D2｝.计算过程如表8－2所示.

表8－2

第三步，k＝2，有方程

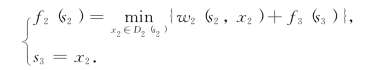
现在S2＝｛B1，B2，B3｝，D2（B1）＝｛C1，C2｝，D2（B2）＝｛C1，C2，C3，C4｝，D2（B2）＝｛C1，C3，C4｝，计算过程如表8－3所示.

表8－3

第四步，k＝1，有方程

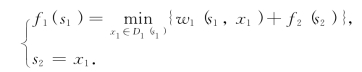
现在S1＝｛A｝，D1（A）＝｛B1，B2，B3｝.计算过程如表8－4所示.

表8－4

根据状态转移方程及表8－1至表8－4，我们用顺序追踪法，即可求得本问题的最优决策序列：

由此可知，旅行者的最佳路线为AB3C3D1E，行程为12.

由上述求解过程可见，本方法是把求A至E的最短路径问题，嵌入到“求各个点至E的最短路径”这一族最短路径问题中，这一族问题与原来的问题是同类型的.这种方法在数学上称为不变嵌入法.同时可见，上述方法所求得的解也是一族，如图8－2那样.

这里，我们应该指出，如果一个实际问题可以归结为最短路径问题，那么，一般都采用网络规划中有关的算法而决不会运用动态规划方法来求解.本节详尽地介绍用动态规划方法来求解最短路径问题，仅仅是以此作为认识和理解动态规划方法的入门.