前面我们所阐述的PERT网络的每道工序的工序时间都是预先确定的.工程组织者参考以前相仿的网络计划的历史资料(例如同类工序的工时定额统计资料),用分析对比的方法对本工程各道工序的作业时间作一个估计.我们称采用这种单一时间估计法估计各道工序作业时间的PERT网络为肯定型网络.
但对随机因素较多的网络计划或无先例可循的网络计划(例如新开发的大型建设工程和科研项目等),其计划实施的技术条件和组织条件的不可知因素较多,不具备各道工序定额工时统计资料,因此,很难确定各工序的工序时间究竟是多少.
工序时间是随机变量的PERT网络被称为非肯定的PERT网络.
我们采用3种时间估计法来估算非肯定型网络各工序的工序时间,即对每道工序的工序时间估计3种时间:
①乐观时间a:在最顺利的情况下完成工序的时间;
②保守时间b:在最不利的情况下完成工序的时间;
③最可能的时间m:在正常情况下完成工序的最可能需要的时间.
假设工序时间这个随机变量服从取值范围从a到b的β分布,因而,此随机变量的期望值μ和方差σ2分别为

我们就将按式(7-17)确定的工序(i,j)的工序时间期望值作为该工序的长度wij,它的方差记为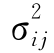 .
.
网络计划的总工期TE是关键路径P中所有工序的工序时间的和,由于工序时间是随机变量,因此TE也是随机变量.现假定各工序的工序时间是彼此独立的随机变量.当关键路径P上工序较多时,根据概率论中的中心极限定理可知,总工期TE服从正态分布,它的数学期望和方差分别为

例7-14 考虑由9道工序组成的某项工程,有关信息如表7-16所示(时间单位:天).试求总工期TE的期望值和方差,以及总工期在50天内完成的概率.
表7-16
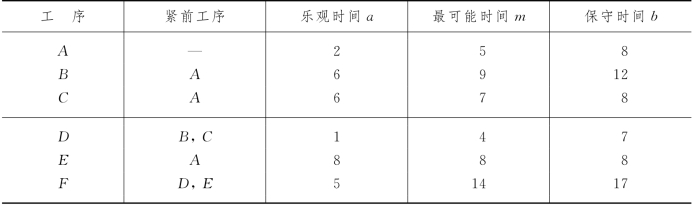
(续表)
 (https://www.daowen.com)
(https://www.daowen.com)
解 经计算,可知各道工序的工序时间期望值和方差如表7-17所示.
表7-17

本问题的网络图如图7-39所示,边(i,j)旁参数为该工序的工序时间期望值wij.
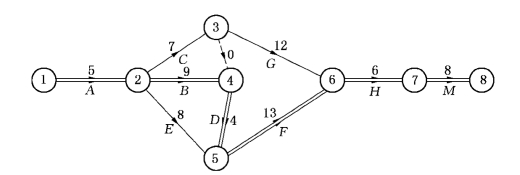
图7-39
可知,关键路径为(1,2)(2,4)(4,5)(5,6)(6,7)(7,8).由式(7-19)和式(7-20)可得
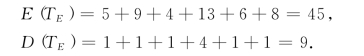
于是,总工期TE服从正态分布N(45,9).由正态分布特性可知,随机变量位于距离数学期望一个标准差以内的概率是0.68,因此
![]()
由于随机变量
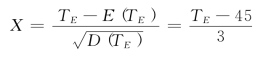
服从标准正态分布N(0,1),所以总工期在50天内完成的概率
![]()
其中Φ(x)为标准正态分布N(0,1)的分布函数
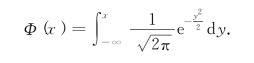
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








