我们不准备对总工期－资源的优化问题作全面的介绍与深入的讨论，而仅仅探讨一下当资源有限制时，如何合理地安排资源.

例7－13　某工程的网络图由图7－34给出.图中有向边旁第一个参数为工序的工序时间wij（单位：天），第二个参数为该工序每天所需要的作业人数.现在假设该项工程由一个工程队承包，全队共有人员12名，且设每个人员都可以胜任各工序的工作.试问，该队对各工序的进度如何安排及如何合理地调配人员，以使工程尽早地完工.

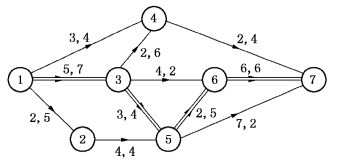
图7－34

该网络图的关键路径为（1，3）（3，5）（5，6）（6，7），其长度TE＝16（天）.各事项的最早时间和最迟时间经计算由表7－11给出，各工序的总时差由表7－12给出.

表7－11

表7－12

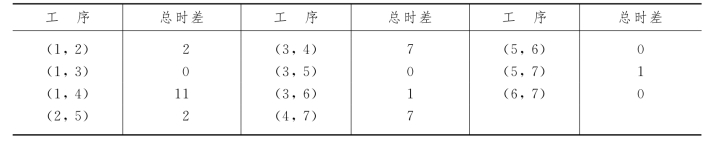
将各工序所需的工作日（每天需要的人员乘以该工序的工序时间）相加，可知该工程共需173个工作日，因此如用16天完成（承包这项工程所需的时间不能小于总工期16天），则平均每天需要投入的人员数为173／16≈11＜12.所以，适当安排各道工序的进程，整个工程有可能在16天内完成（反之，要是平均每天需要投入的人员数超过12，则不论如何安排整个工程各工序的进度，均无可能在16天内完成该项工程）.

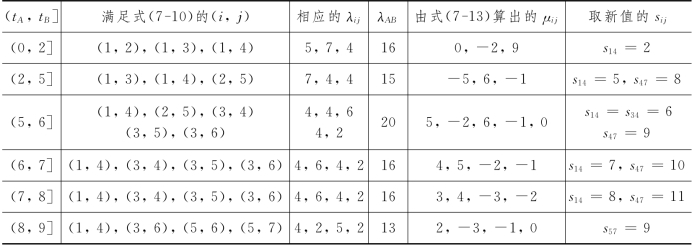
如果将每道工序（i，j）都安排在第tE（i）＋1天开始执行，可得一张表示工程进度的横道图，如表7－13所示.表中“”表示关键工序的进度；“——”表示非关键工序的进度；横道线上的数字表示执行该工序时每天所需的人员数；“……”表示在不误总工期的条件下，非关键工序的执行时间所允许的变动范围（例如，工序（3，4）所需的两天时间可安排在第6天初至第14天末这个时间区间内任何持续的两天）.

表7－13

从表7－13可以看出，由于各工序均按其最早开工时间安排进度，因此工程的前期人员的需求较多，而工程后期人员的需求较少，整个工程进行期间人员的需求很不均匀.图7－35为按照横道图表7－13所得的人员资源需求曲线，这是一条阶梯形曲线.图7－35告诉我们，有5天超出了目前人员资源的限制条件.

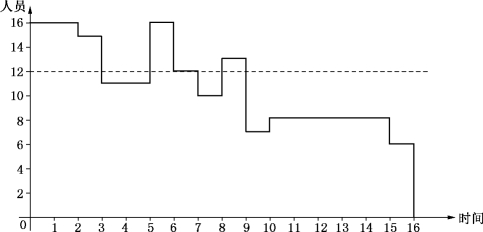
图7－35

于是，我们就要在保证总工期16天不变的条件下（对有些问题，可能要适当地调整原定的总工期，以保证资源的合理使用），调整各工序的进度，使人员需求尽可能地平衡，且不超过每天可配备的人员数.对每天人员使用量（或资源）调整的基本原则是：

首先，将人力（或资源）优先分配给关键工序和总时差较小的工序；

然后，利用非关键工序的总时差，调整各道非关键工序的开工时间.对能够推迟开工的工序，适当地向后推迟.

下面我们对这类资源附有限制的网络计划问题作一般的讨论.

假若网络计划问题所需要的某种资源在单位时间内的最大供应量为λmax，那么，在此资源限制条件下，可以按以下步骤求总工期最短的计划方案.

①当网络图给定后，先求出有关的时间参数及总工期TE.将每道工序（i，j）都先安排在tE（i）＋1天开始执行，由此绘制横道图，得到一条阶梯形的资源需求曲线.该曲线任何一个梯段的开始或结束，均意味着有某些工序开工或完工.

②对资源需求曲线自左至右按梯段进行检查，如资源需求超过资源最大供应量λmax，就要加以调整.利用非关键工序的总时差，错开它们的开工时间，分散对资源需求的压力，力争在总工期TE内完工.

例如某网络计划经过多次网络分析后，有资源需求曲线如图7－36所示，λ为资源需求量.此时，假设每道工序（i，j）的开工日期为第sij＋1天，（tA，tB］为该曲线首先超出λmax的阶梯所在的时间区间，λAB为此阶梯的高度.

显然，时间区间（tA，tB］内的若干工序（i，j）必满足下面两个条件：

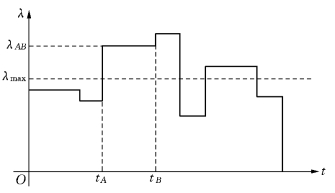
图7－36

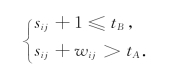
（tA，tB］内的工序（i，j）如图7－37所示，这些工序有

在图7－37所示的这些工序中，我们若能利用工序（i，j）的总时差，把工序（i，j）的开工日期后移到第tB＋1天（即取sij＝tB），则将减少（tA，tB］时间区间内对资源的需求量.但是，这样做时应尽可能不影响总工期（或使总工期延长时间最少），故要求

(www.daowen.com)

图7－37

现令

由图7－38可知：当μij＜0时，取sij＝tB将会影响整个工程按原定总工期完工，这时｜μij｜表示新的完工期比总工期延长的天数.当μij≥0时，说明取sij＝tB将不影响总工期，这时｜μij｜表示取sij＝tB后，工序（i，j）的开工日期还剩余的机动天数.我们对式（7－12）进行变换：

图7－38

那么，在满足式（7－10）的各道工序（i，j）中，应挑选哪些工序，使其开工日期后移到第tB＋1天呢？

一般来说遵循如下3条原则：

①优先挑选μij大的工序（i，j），使它的开工时间sij＝tB.因为当μij≥0时，μij越大说明工序（i，j）的开工时间后移后仍有较多的开工剩余机动时间；当μij＜0时，μij越大，则｜μij｜越小，说明工序（i，j）的开工时间后移后使总工期拖延的天数越小.

②为了减轻工程后期施工对资源需求的压力，一般不宜把过多的资源需求量推迟.最好是在满足资源限额的条件下，使资源的利用尽量均衡些.

③当sij的数值改变后，对于以事项j为开工事项的工序（j，k）来说，若sjk＜sij＋wij，则（j，k）工序已不能按原订的日期第sjk＋1天开工，这时，应取sjk＝sij＋wij.同样地，对于以事项k为开工事项的工序，其开工日期也应作相应改变，其余工序依此类推.

有时，我们可将某些满足式（7－10）的工序（i，j）在时间区间（tA，tB］内中断工作，或延长其工序时间，以达到使资源需求量减少的目的.

我们根据上述原则来改变一些工序的开工日期，并修改原来的进度表，得到新的资源需求曲线.再重复上述步骤，直到资源需求曲线的所有阶梯的高度都不超过λmax为止.

本方法的计算工作量十分繁重.对于大中型网络，只能依靠电子计算机来进行.

下面我们来求解例7－13.

我们用表7－13所示的进度表，用上述方法逐步调整一些工序的进度.在调整过程中，进度表的修改可以在原来的基础上进行.资源需求曲线的引入，是为了直观地分析超出资源限额的情况.在实际调整过程中，不一定要画出资源需求曲线.事实上，时间区间（tA，tB］和λmax都可以直接从横道图相应的进度表中得到.利用表7－13，我们对调整过程中时间区间（tA，tB］中满足式（7－10）的工序（i，j）相应的μij进行计算，并把有关计算过程列成表7－14，其中λij为工序（i，j）每天所需人员数.例如表7－14的第二行（tA，tB］＝（2，5］，此时满足式（7－10）的工序有（1，3），（1，4），（2，5），因此：

表7－14

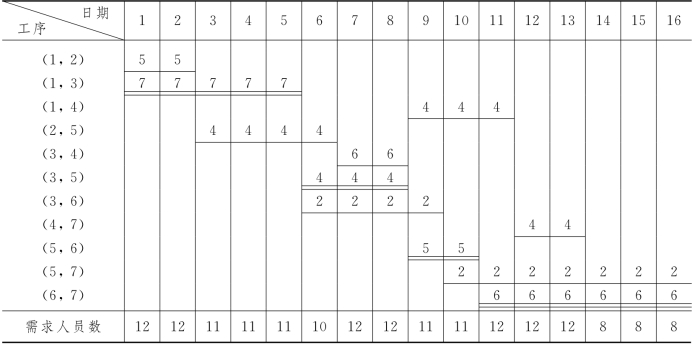
由表7－14可知，应取s14＝8，s34＝6，s57＝9，s47＝11，其他sij＝tE（i）.对表7－13进行修改，可得新的横道图，如表7－15所示.由这张进度表可知，总工期仍为16天.

表7－15

那么，如何评价一个工程进度表对资源利用的均衡性呢？下面我们来讨论此问题.

若工程进度计划表确定后，用λ表示第t天对资源的需求量，T为进度表相应的总工期，则日资源利用量的均值为

我们的问题就成为在计划工期T固定的条件下，找到一种进度计划使S2取极小值.一般可采用如下的试探法：

先求出网络图的时间参数，把每道工序（i，j）的开工日期都安排在第tE（i）＋1天.于是得到一张初始进度计划表，计算相应的S2.然后利用非关键工序的总时差，依次对每道非关键工序的执行时间作试探性调整，若调整后的S2值减少，则接受这个调整措施，从而获得一张新的进度计划表.重复上述过程，直到求得某一进度计划时，对每道非关键工序的试探性调整已无法使S2减小，此时，即终止调整工作.

对于图7－34网络所示工程来说，表7－13所给的进度计划表相应的S2＝11.40，可见该进度计划的资源利用是很不均衡的.表7－15所给的进度计划表相应的S2＝2.15，可见，该进度计划的资源利用就比较均衡了.