一项工程的成本，一般可分为直接成本和间接成本两大类：

（1）直接成本：如人工、原材料、燃料和机械设备租用等直接与工序工作有关的费用.直接成本要分摊到每道工序上.

（2）间接成本：如管理人员工资、行政办公费、采购费、劳保福利费等.间接成本不分摊到每道工序上而作为整个工程的成本.显然，总工期TE短，间接成本就低.

对某些工程问题，在确定总工期后，常常需要对某些工序考虑赶工的措施（例如增加人员或增添设备、改进原材料及采用新技术等），以缩短这些工序的施工时间，从而使总工期缩短.此时，虽然由于工序赶工而增加赶工费用使工序成本增加，从而使直接成本增加，但因为总工期的缩短，又使间接成本减少，从整体来说经济效益可能会更好些.

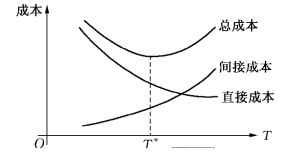
图7－16

直接成本、间接成本和总成本（直接成本与间接成本之和）与总工期的关系如图7－16所示.可见，图中总成本曲线是一个马鞍形曲线，其中，最低点（鞍点）所对应的总工期为总成本最低的总工期，称为最优总工期，记为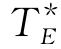.所以，若要求最低成本的最优总工期，不妨先固定总工期TE，然后确定成本最低的计划方案，再让TE在某一个范围内变化，比较不同总工期TE所对应的总成本，即可求得.

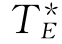1.指定总工期的成本优化问题

若PERT网络确定的总工期为TE，现指定一个总工期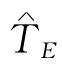（＜TE），我们来考虑成本优化问题.

由于总工期固定为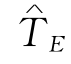（称为指定总工期），所以间接成本是固定的，故成本最低意味着各工序的直接成本总和最低.又由于每道工序成本由正常成本及赶工费用组成，所以直接成本总和最低也就是意味着各工序的赶工费用总和最低.对于指定总工期的成本优化问题，我们介绍枚举法、负时差法和线性规划法.

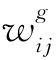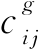为了估算的方便，常常假定在工序成本与工序时间之间有着线性的关系，如图7－17所示，其中和分别表示在正常情况下工序（i，j）的作业时间和所需成本（分别称为工序的正常工序时间和正常成本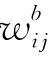）；和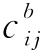分别表示工序（i，j）的赶工时间限度和相应的成本.

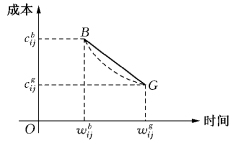
图7－17

赶工成本斜率——工序（i，j）缩短一个单位时间所增加的直接成本称为该工序的赶工成本斜率，记为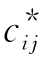.即工序（i，j）的赶工成本斜率.

下面我们给出总工期指定为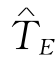时的成本优化问题的求解方法（若每道工序（i，j）都采用它的时间限度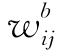作为它的长度，求得相应网络的总工期为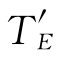，则应有）.

（1）枚举法.我们首先对网络图中各工序的工序时间在取为正常时间时求出工程的总工期TE，若TE大于指定总工期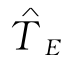，则就要采取赶工措施.我们面临的问题是，应该在哪些工序上赶工，被赶工的工序的施工时间为多少，才能使所增加的赶工费用最少.下面通过具体的例子来说明枚举法的赶工思想.

例7－4　某工程的有关信息由表7－3给出.已知间接成本每天500元，若指定总工期＝21天，试由赶工成本和间接成本来考虑本工程的最优赶工方案.

表7－3

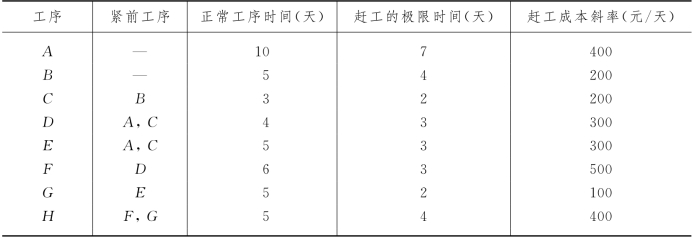
解　如果所有工序都以正常时间完工，我们给出本工程的网络图7－18，此时总工期TE＝25天，赶工成本与间接成本之和

图7－18

在图7－18中，有两条关键路径P1＝A—D—F—H和P2＝A—E—G—H.

若先将总工期25天压缩为24天.为此，我们就要采取赶工措施分别缩短关键路径P1和P2的长度1天.换言之，必须压缩关键工序的工序时间，对关键工序进行赶工.显然，我们首先应考虑对两条关键路径的共同工序中赶工成本斜率最小的关键工序进行赶工.P1和P2有两道共同工序H和A，赶工成本斜率都为400元.我们取关键工序H进行赶工，对其工序时间w67压缩至它的极限时间4天.此时，赶工的成本为400元，另一方面，由于总工期从25天压缩至24天，间接成本可节省500元.

由于指定总工期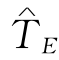＝21天，我们必须再对关键工序进行赶工.现在我们考虑对两条关键路径的共同工序A进行赶工.但是工序A不能压缩到它的极限时间7天，否则路径P3＝B—C—D—F—H和路径P4＝B—C—E—G—H上升为关键路径，它们的长度为8天，而原关键路径P1和P2不再是关键路径，这样的赶工将是不经济的.所以，我们仅对工序A的工序时间压缩2天，其赶工成本为800元.此时，工序B和C也都成了关键工序，路径P1，P2，P3和P4都是关键路径（如图7－19），它们的长度都为22天，间接成本节省1 000元.

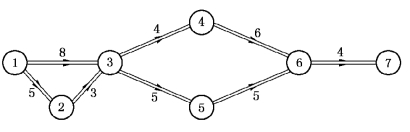
图7－19

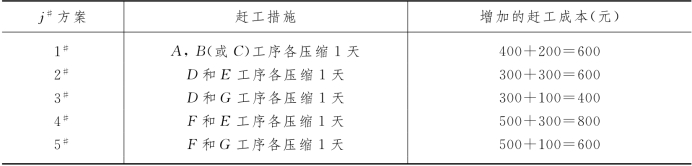
为了实现工程的总工期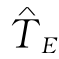＝21天，我们必须继续赶工，将现有的总工期22天压缩至21天.表7－4给出了各种可能的组合方案，可见3＃方案最经济.于是，我们将D和G这两道工序都压缩1天，赶工成本为400元，间接成本节省500元.

表7－4

综上讨论，在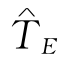＝21天时，我们将最合理的赶工方案列成表7－5.此时，赶工成本和间接成本之和

表7－5

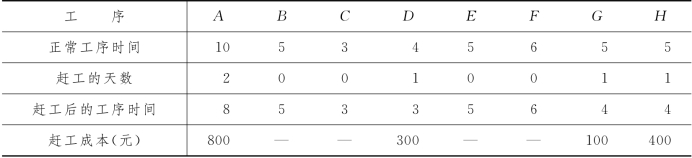
总工期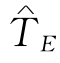＝21天的网络图由图7－20给出.

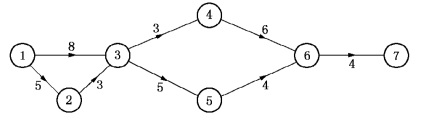
图7－20

通过上述实例的分析，可见，指定总工期为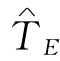的成本优化问题，可通过对各工序长度都为正常时间的网络进行合理赶工来求解.赶工措施的原则为：

①在关键路径上，对赶工成本斜率最低的工序采取赶工措施；

②在关键路径赶工后，其他非关键路径有可能上升为关键路径.在今后赶工中，则对新的关键路径的有关工序也应进行赶工，但必须应使原有的关键路径继续保持为关键路径.

③数条关键路径同时赶工时，应首先考虑共同工序赶工，并以支付最低的赶工成本为目的.

例7－5　现给网络如图7－21.各工序的正常工序时间、正常成本、赶工的极限时间、赶工成本斜率如表7－6所示（表7－6中“＊”表示无论投入多少资金，亦无法缩短该工序的工序时间）.现在取指定总工期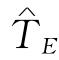＝23天，问如何赶工以使赶工成本最低.

解　第一步，在图7－21中关键路径为（1，2）（2，3）（3，5）（5，6），其长度为26天，大于指定总工期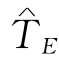＝23天.于是，我们采取赶工措施.

首先选择关键路径上赶工成本斜率最低的工序（2，3）压缩2天（由表7－6知，工序（2，3）至多压缩2天），增加赶工成本60×2＝120元，得新的网络如图7－22，它有3条关键路径：

它们的长度都为24天.

表7－6

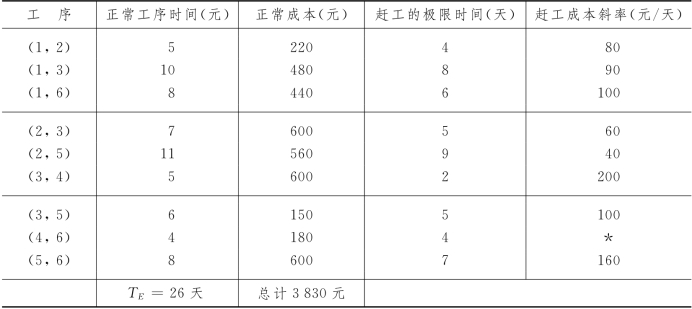
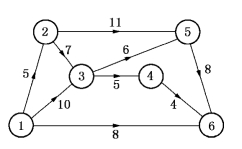
图7－21

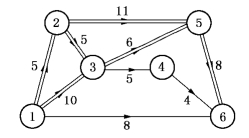
图7－22

第二步，对网络图7－22来说，TE＝24天，为实现指定总工期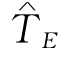＝23天，必须对关键路径P1，P2和P3的长度都压缩1天.我们将这3条关键路径的有关工序及其赶工成本斜率列成表7－7.

表7－7

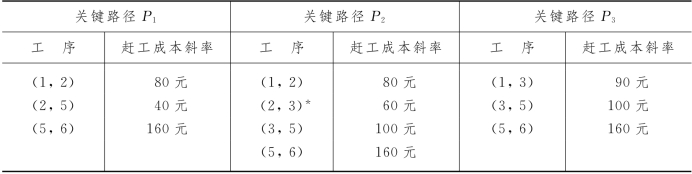
（＊：P2的关键工序（2，3）不能再压缩）

现在将这3条关键路径长度各压缩1天，对关键工序赶工一天的组合情况及其赶工成本列成表7－8.可见，2＃方案赶工成本最少.此时，工序（2，5）压缩1天，赶工成本40元，工序（3，5）为关键路径P2与P3的共同工序，压缩1天，其赶工成本为100元，合计140元.按2＃方案所得的网络如图7－23.

表7－8

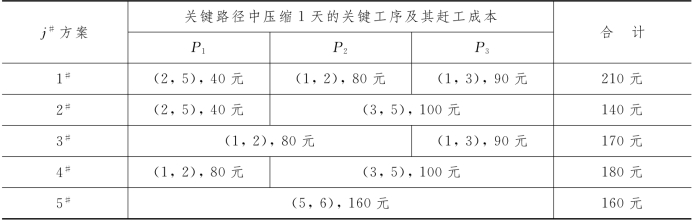
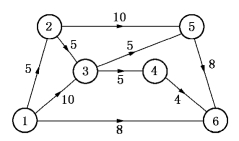
图7－23

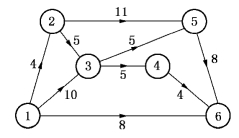
图7－24

从表7－8看，4＃方案不如2＃方案.如果采用4＃方案赶工，其网络图如图7－24.

第三步，现若由网络图7－21的总工期26天直接压缩为23天，则当为图7－23时，赶工成本为40＋60×2＋100＝260（元），而为图7－24时，赶工成本为80＋60×2＋100＝300（元）.

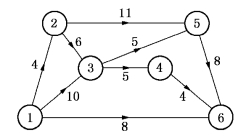
图7－25(www.daowen.com)

但在图7－24中，我们可以发现，图7－21中的关键路径（1，2），（2，3），（3，5），（5，6）此时已不是关键路径，（2，3）不再是关键工序，可知工序（2，3）的总时差R（2，3）＝1，故在图7－24中工序（2，3）的工序时间取为6天也不影响工程在23天完成.所以总工期由26天直接压缩为23天时，我们将图7－24中工序（2，3）的工序时间改为6天，相应的网络如图7－25所示，它的赶工成本为300－60＝240（元）.显然，网络图7－25相应的赶工措施要比图7－23和图7－24相应的赶工措施来得好.

因此，当指定总工期为23天时，赶工成本最低的最佳赶工措施是从图7－21化为图7－25：工序（1，2），（2，3），（3，5）分别压缩1天，赶工成本分别为80元，60元和100元，总的赶工成本为80＋60＋100＝240（元）.

从上述两个例题的求解过程可看出，枚举法只适用于小型工程计划，对于庞大的工程计划，枚举法就无能为力了.

（2）负时差法.给PERT网络N＝（V，E，W，①，ⓝ），若对（i，j）∈E，在取wij为正常工序时间时，工序（i，j）的总时差为R（i，j），工程的总工期为TE.

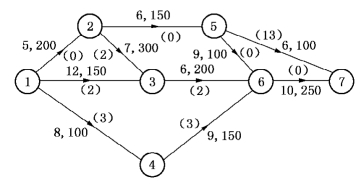
图7－26

图7－27

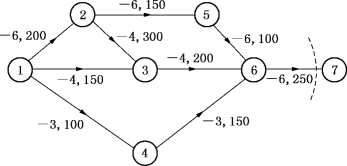
图7－28

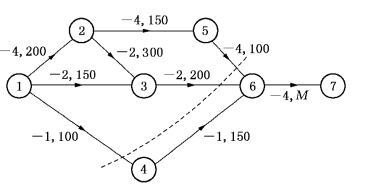
图7－29

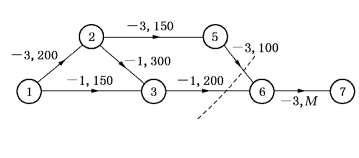
图7－30

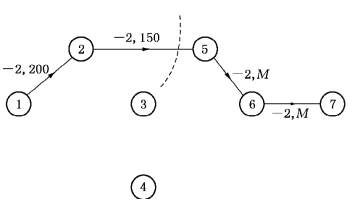
图7－31

图7－31给出了网络N4，相应的δ1＝－2.可知

现取δ＝－2，在N中取w25＝4，其赶工成本为150×2＝300.这时，ΔTE＝0.

所以，当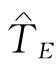＝24时，在采用最佳赶工方案后，各工序的工序时间如图7－32所示，赶工成本＝500＋400＋300＋300＝1 500.

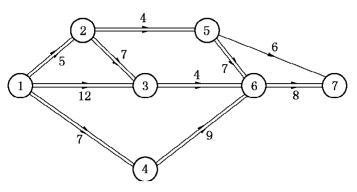
图7－32

在这个例子中，所选取的赶工工序（6，7）是4条关键路径的共同工序，工序（3，6）是2条关键路径的共同工序，可见共同工序经常在最小割中.

但是，这里要指出，用上述算法求解某些指定工期成本优化问题时，得到的不一定是最优赶工方案.这是因为Nk中的最小割不一定唯一，且最小割中边的负时差未必相同.感兴趣的读者可对此算法作进一步探讨.

例如，如果用上述算法对例7－5的图7－21进行赶工，则得网络图7－23，赶工成本为260元（请读者作为习题求解）.

（3）线性规划法.对于大型PERT网络的总工期—成本优化问题，可以通过建立线性规划模型来进行最优决策.让我们先来讨论一个简单的例题，分析一下线性规划模型是如何对PERT网络求关键路径及总工期的.

例7－7　给PERT网络如图7－33所示.试用线性规划方法求该网络的关键路径及总工期.

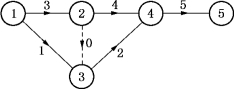
图7－33

解　设ti为事项i发生的时间（例如t1表示工程开始的时间，t5表示工程完工的时间，t4表示工序（2，4）及（3，4）都完工的时间.即ti是以顶点i为终点的工序的完工时间中的最大值）.

显然，对于网络中的每条边（i，j）都有一个相应的约束条件tj－ti≥wij，以保证工序（i，j）安排作业的可用时间不小于该工序的工序时间wij.于是，我们得下列线性规划模型：

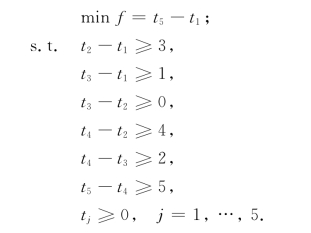
用单纯形法对该模型求解，最优解和最优值分别为

因此，该PERT网络的总工期TE＝12天.在最优解中，使约束条件取等式的相应工序意味着该工序的开工日期没有机动时间，所以这些工序即为关键工序.例如：

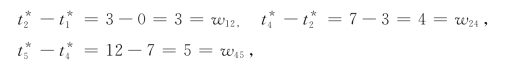
因此，工序（1，2），（2，4），（4，5）为该网络的关键工序.令

kij——工序（i，j）的正常工序时间；

lij——工序（i，j）赶工的极限时间；

cij——工序（i，j）赶工一天的成本；

wij——工序（i，j）的实际工作时间；

tj——事项j的发生时间.

对PERT网络的总工期—成本优化问题，我们根据不同的目标，给出下列3个线性规划模型.

例7－8　现要求工程的总工期应不迟于T.为使赶工总成本最小，问如何安排各工序的进度？

解　本问题的线性规划模型为

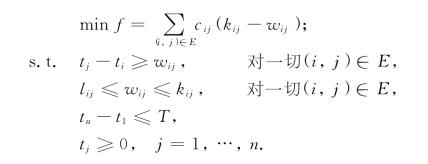
例7－9　为使总工期压缩，现增加投资b，问对哪些工序进行赶工，以使总工期最小？

解　本问题的线性规划模型为

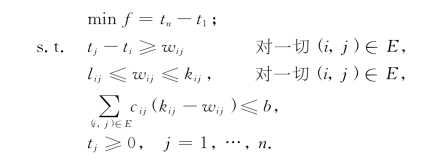
例7－10　若工程每天的间接成本为d元.为使间接成本和赶工成本之和最小，问如何安排各工序的进度.

解　本问题的线性规划模型为

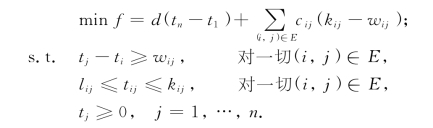
2.最低成本的最优总工期问题

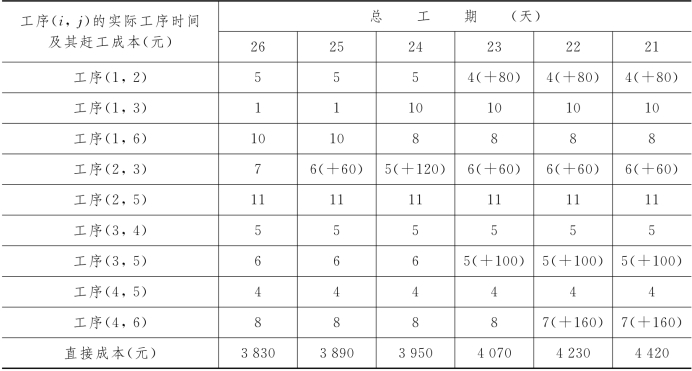
例7－11　给出例7－5不同总工期的赶工方案并计算相应的直接成本.

解　我们将有关计算结果列成表7－9（若各工序都取其赶工的极限时间，则可知相应的总工期为21天，直接成本为5 350元，我们没有列进表7－9中）.

表7－9

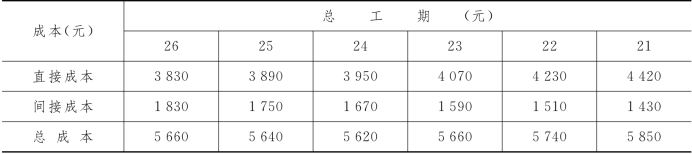
例7－12　对例7－11，若在TE＝26时，知其间接成本为1 830元.当总工期每压缩1天，间接成本可节省80元，求总成本最低的最优总工期.

解　利用表7－9的有关信息并计算不同总工期时的间接成本，我们可算得不同总工期相应的总成本，如表7－10所示，可见总成本最低的最优总工期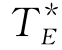＝24天.

表7－10