如果我们在图7－11的12个事项中任取一个事项，例如取事项5，那么它作为工序（5，8）的开工事项，最早可在整个工程开工几天后执行呢？显然，事项5作为开工事项一定要等工序（1，5）和（3，5）都完工后才能执行，仅工序（1，5）完工后还不能执行开工事项5.从图上可以看出，事项5最早可在开工14天后（第15天）执行.

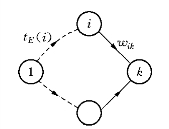
图7－12

为此，我们对于网络图中任一个事项k引进第一个时间参数：

事项k的最早时间tE（k）——从顶点1到顶点k的最长路径长度称为事项k的最早时间，记以tE（k）.

tE（k）的实际意义是指：以事项k为起点的工序必须等它的紧前工序都完工后才能开工，它们的预期最早执行时间在整个工程开工tE（k）天后（即在第tE（k）＋1天）.

在图7－12中，工序（i，k）是以k为终点的工序之一（根据编号原则，有i＜k），wik为工序（i，k）之长度，tE（i）为顶点1至顶点i的最长路径长度，虚线表示相应的最长路径.由图7－12不难得到下列递推公式：

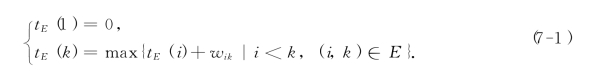
总工期——事项n的最早时间tE（n）称为工程的总工期，记作TE.

TE表示整个工程从开工到完工所需的最少时间.

由图7－11可知，tE（12）＝23，tE（7）＝19，事项7作为工序（7，12）的开工事项，如果在整个工程开工21天后工序（7，12）还不开工，那么整个工程的完工时间就将超过23天，因为执行工序（7，12）需要2天时间.为此，我们引进事项k的第二个时间参数：

事项k的最迟时间tL（k）——总工期TE与顶点k至顶点n的最长路径长度之差称为事项k的最迟时间，记为tL（k）.

tL（k）的实际意义是指：在不误总工期TE的前提下，以事项k为开工事项的工序最迟应在整个工程开工tL（k）天后执行，也即以事项k为完工事项的工序最迟完工的时间为第tL（k）天.

在图7－13中，工序（k，i）是以k为起点的工序之一，TEtL（i）为顶点i至顶点n的最长路径长度，虚线表示相应的最长路径.由图7－13可得下列递推公式：

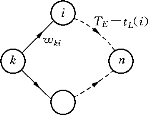
图7－13

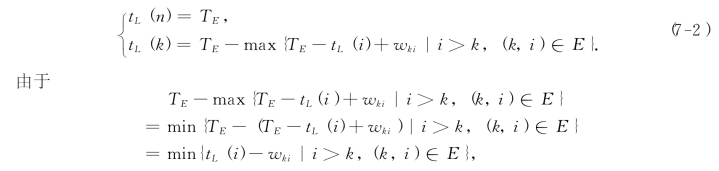
所以式（7－2）化成下列形式：

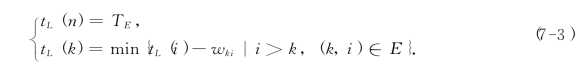
关键路径——PERT网络N中从顶点1至顶点n的最长路径为网络的关键路径（可能不止一条），其长度即为TE.关键路径上的工序称为关键工序.

关键事项——若对于事项k有tE（k）＝tL（k），则称事项k为关键事项.

例7－2　求图7－11所示PERT网络各事项的最早时间、最迟时间及关键路径.

解　应用公式（7－1）从tE（1）＝0出发逐个求出tE（2），tE（3），…，tE（12）.再应用公式（7－3）从tL（12）＝TE出发，逐个求出tL（11），tL（10），…，tL（1）.具体计算结果见图7－14（顶点k旁正方形框中标出的数字为tE（k），三角形框中标出的数字为tL（k））.例如：

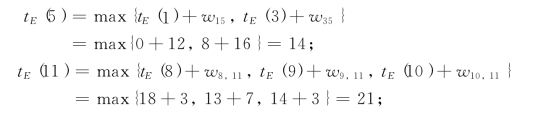
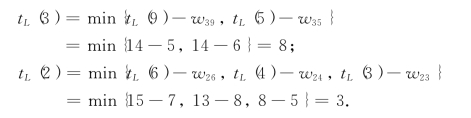(www.daowen.com)

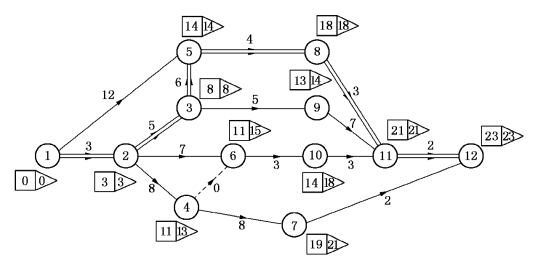
图7－14

图7－14中双线所示路径（1，2）（2，3）（3，5）（5，8）（8，11）（11，12）即为关键路径.

利用事项的最早时间和最迟时间，我们给出工序（i，j）的6个时间参数：

工序（i，j）的最早开工时间——tE（i）即为工序（i，j）的最早开工时间.

工序（i，j）的最早完工时间——tE（i）＋wij即为工序（i，j）的最早完工时间.

工序（i，j）的最迟完工时间——tL（j）即为工序（i，j）的最迟完工时间.

工序（i，j）的最迟开工时间——tL（j）－wij即为工序（i，j）的最迟开工时间.

工序（i，j）的总时差——在不延长总工期的前提下，工序（i，j）完工期的机动时间称为工序（i，j）的总时差，记为R（i，j）.

显然，R（i，j）是工序（i，j）的最迟完工时间与最早完工时间之差（或为最迟开工时间与最早开工时间之差），因此，有

工序（i，j）的单时差——在不影响紧后工序最早开工时间的前提下，工序（i，j）的完工期的机动时间称为工序（i，j）的单时差，记为r（i，j）.

显然，r（i，j）为工序（i，j）的紧后工序的最早开工时间tE（j）与工序（i，j）的最早完工时间之差，因此，有

关于工序（i，j）的6个时间参数之间的关系可用图7－15来说明.

下列结论显然成立.

定理7－1　工序（i，j）为关键工序的充分必要条件为R（i，j）＝0.

例7－3　计算图7－14各工序的6个时间参数.

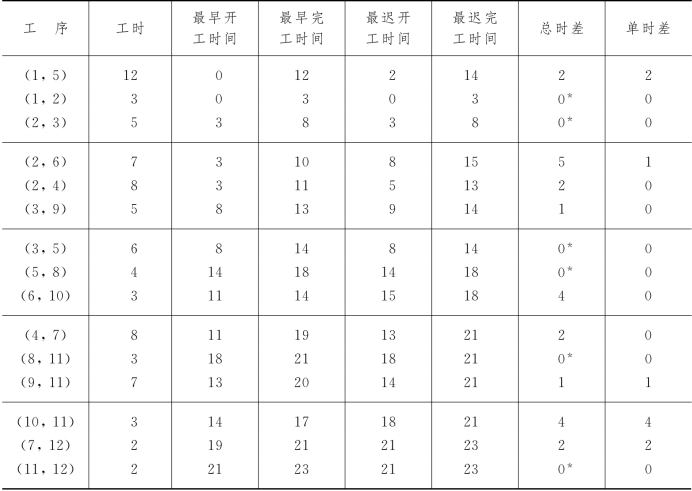
解　具体计算结果由表7－2给出（表中总时差打＊者相应的工序为关键时序）.

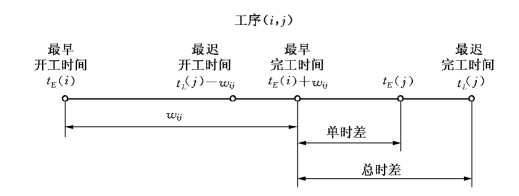
图7－15

表7－2