一项工程总是由许多相互独立的活动组成的，今后称这些活动为工序.各道工序之间有着一定的先后次序上的联系，且完成各道工序都需要耗费一定的时间（不妨设单位时间为天），称它们为工序的长度或工序时间.我们可以采用一个赋权有向图来描述工程各道工序之间相互依存的逻辑关系：

①以一条有向边来表示一道工序，有向边的权即为此工序的长度；

②有向边的起点和终点分别表示相应工序的开工和完工，称为事项；

③前接工序的完工事项即为后继工序的开工事项.

我们称这种赋权有向图为计划网络图，简称网络图.

下面给出网络图的绘制规则和方法：

（1）若工序D和E必须在工序A、B和C完成后才能开工，可用图7－1表示.称工序A、B和C为工序D或工序E的紧前工序，工序D（或E）称为工序A（或B或C）的紧后工序.

（2）若工序C需工序A及B完工后始能开工，而工序D在工序B完工后就可开工，此时，在工序B和C之间虚设一个长度为0的“虚工序”，如图7－2所示.这种虚工序在任务实施中实际上是不存在的，只表示工序之间的逻辑关系，它不耗费时间和资源.

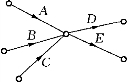
图7－1

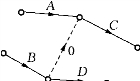
图7－2

（3）网络图中不允许出现平行边.

在使用电子计算机对网络图进行有关的时间参数计算时，一般都利用有向边的起点及终点的编号来表示有向边.因此，在具有平行边的网络图中，当起点、终点的编号给定后，边不能唯一地确定.所以，图7－3的形式在网络图中是不允许的.我们可以利用虚工序的技巧，用图7－4来表示图7－3中工序之间的逻辑关系.

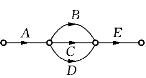
图7－3

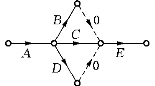
图7－4

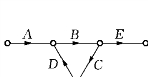
图7－5

（4）网络图中不允许出现回路.

例如，图7－5中存在回路，工序流程出现循环，这是逻辑上的错误，不允许出现.

（5）网络图中只能具有一个源（工程的始点，它只具有输出边）和一个汇（工程的终点，它只具有输入边），即自网络图的源出发经由任何路径都可以到达汇.

例如图7－6这种形式是错误的.如果图7－6作如此解释：工序A和B可以同时开工，工序F和H完工后工程即告完成，则应画成图7－7形式.

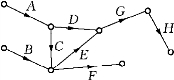
图7－6(www.daowen.com)

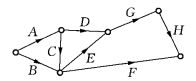
图7－7

于是，一个工程就可用一个网络N＝（V，E，W，x，y）来描述，它没有平行边，没有回路，源x表示工程的总开工事项，汇y表示工程的总完工事项，W（e）表示工序e的长度.我们称这一网络N为该工程的PERT网络.

对PERT网络N的每个顶点需用数字进行编号.若N中有一条以u为起点、v为终点的有向边（u，v），则顶点u的编号i应小于顶点v的编号j，并且就以边（i，j）表示该工序（u，v），其长度记为Wij.

我们可按如下方法对顶点进行编号：首先给源x以编号1（以后用①表示源），接着设想把以源为起点的边都从网络N中删去，这样得到一个或数个没有输入边且未编号的顶点，对它们逐一编上号（对这些顶点来说，编号的前后顺序无关紧要）.然后再从N中把以这些新编上号的顶点为起点的边删去，又得到一些没有输入边的未编号的点，再逐一地编号.如此继续进行，直至最后一个顶点汇y被编上号（假设为n，以后就以ⓝ来表示汇）.

今后，我们将直接用顶点的编号来称呼顶点或事项.

在绘制一项工程的PERT网络时，首先要把整个工程分解成若干道工序（工序是在工艺上和生产组织管理上具有相对独立性的活动）并确定工序的长度，然后根据工艺流程确定各工序之间的顺序关系.

由于工程设计的图纸一般总有总图和分图等不同的层次.因此，对于规模较大的工程，在编制网络图时，同样地也应分成层次，区分为网络总图和网络分图.网络分图在网络总图中可以用一道工序来表示，其长度为网络分图中最长路径的长度.

有时，为了加快工程进度，对于相邻的工序，可以不必待紧前工序全部完工后才开始下一道工序，可以先完成前道工序的一部分作业，然后就开始紧后工序的一部分作业.换言之，在条件许可下，把一些相邻的若干工序进行分解，采用交叉作业.

例如：①原工序B紧接工序A，现在A工序分解成A1，A2和A3，B工序分解成B1，B2和B3，则可画成图7－8.

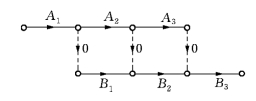
图7－8

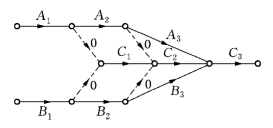
图7－9

②原工序C紧接工序A和B，现在A分解成A1，A2和A3，B分解成B1，B2和B3，C分解成C1，C2和C3，则可画成图7－9.

③原工序A，B，C，D为依次前后紧接的4道工序，现在A，B，C，D分别分解成Ai，Bi，Ci和Di（i＝1，2，3）.则可画成图7－10.

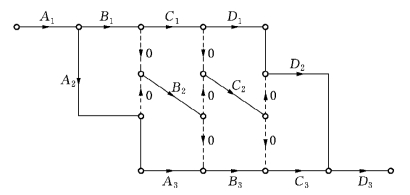
图7－10

例7－1　某工程各工序的顺序关系及各工序的工序时间如表7－1所示，画出它的PERT网络.

表7－1

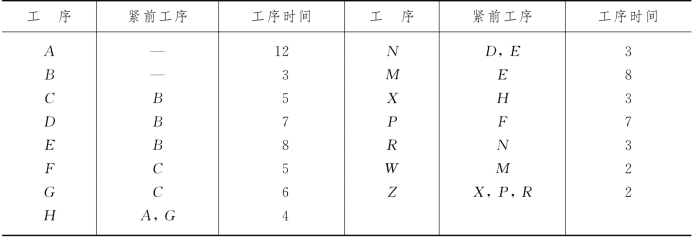
解　该工程的PERT网络如图7－11所示.

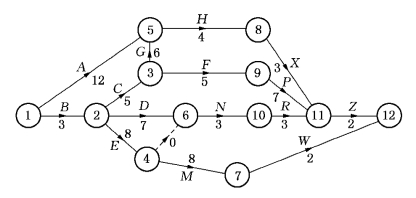
图7－11