最小代价流算法，不仅可以对运输问题建立网络模型进行求解，而且也可以对生产计划问题、多阶段存储问题等一类决策问题建立网络模型并进行求解.下面介绍几个典型例子，从中可见采用网络方法来建立模型时给我们描述问题所带来的方便.

例6－43　（运输问题）　现有两个煤矿x1和x2，每月分别能生产煤13及15个单位，每单位煤的生产费用分别为5及3个单位；另有两个电站y1及y2，每月需用煤分别为12及15个单位.从xi至yj每单位煤的运费wij如表6－41所示.问每个煤矿应生产多少单位煤并如何运输，才能满足y1及y2的需求并使生产和运输总费用最低？

表6－41

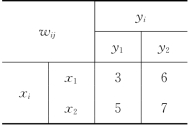
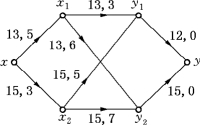
图6－95

解　作网络N＝（V，E，C，W，x，y）如图6－95所示（边旁参数为C（e），W（e），以下各例同）.

由于在x1及x2处分别有13及15个单位的煤可以发出，故边（x，x1）及（x，x2）的容量分别为13及15，W（x，x1）和W（x，x2）分别为x1及x2处每单位煤的生产费用5及3.显然，

而wij（i，j＝1，2）由表6－41给定.由于煤运送到y1或y2后本问题没有进一步考虑其他费用，故W（y1，y）＝W（y2，y）＝0.因为y1及y2分别需要煤12和15个单位，所以C（y1，y）＝12，C（y2，y）＝15.

这样，我们的问题就归结为求图6－95中x至y的最小代价的最大流.

例6－44　（缺货问题）　现有3个汽车配件厂x1，x2，x3，欲将配件运往3个汽车修配厂y1，y2，y3.若修配厂需要的配件得不到满足，就要形成缺货损失费.设y1处不能缺货，y2，y3处每缺一个单位配件就分别造成缺货损失费2和3.其他有关参数如表6－42所给.问如何调配，使总的费用最低？试建立网络模型.

表6－42

解　建立网络模型如图6－96所示.

对i＝1，2，3，取C（x，xi）＝ai，W（x，xi）＝0；对j＝1，2，3，取C（yj，y）＝bj，W（yj，y）＝0.

若表6－42中，xi处不能有配件运至yj，则网络中就没有有向边（xi，yj）.对i，j＝1，2，3，若有边（xi，yi）∈E，则取C（xi，yj）＝ai（或bj），W（xi，yj）＝wij.

图6－96

考虑到供应量之和＝13，需求量之和＝15，供需不平衡，缺少两个单位配件的供应量并需考虑yj（j＝2，3）的缺货损失费，为此虚设一个发点x4，其供应量a4为缺货量2，于是C（x，x4）＝2，而W（x，x4）＝0.因为y2和y3处允许缺货，所以给有向边（x4，y2）及（x4，y3），其容量都为2，而W（x4，y2）和W（x4，y3）分别为y2及y3处的单位配件缺货损失费2和3.因为y1处不允许缺货，所以没有边（x4，y1）.

对图6－96，若用最小代价的最大流算法求得最大流f＊，自然，有Valf＊＝15.

若是f＊（x4，y2）＞0，这意味着y2处缺货f＊（x4，y2），y2处实际收量为6－f＊（x4，y2）；

若是f＊（x4，y2）＝0，这意味着y2处不缺货.对于y3可以作类似的分析.

例6－45　设有x1，x2和x33个化肥厂供应y1，y2和y33个地区的农用化肥，有关参数如表6－43所示.假设3个化肥厂的化肥供应量a1，a2和a3必须全部运完.试建立网络模型，以使总运费最省.

表6－43

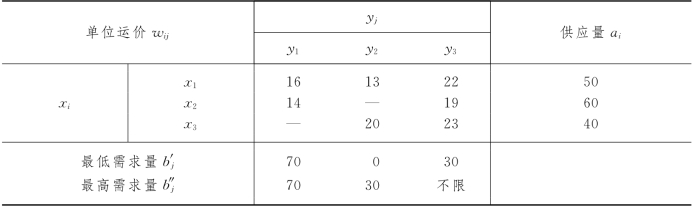
解　由于3个化肥厂的化肥供应量之和＝150，而3个地区的化肥最低需求量之和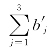＝100，故y3的化肥最高需求量

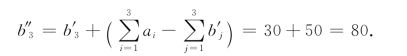
又3个地区的化肥最高需求量之和

把有关点相关联并给出有关参数，即得网络模型如图6－97所示.

图6－97

例6－46　对例1－20所给的生产计划问题建立网络模型.

解　设x为源（工厂），y为汇（销售公司）.又设vi为第j季度产品的存储与供货点（j＝1，2，3，4）.

第一季度工厂的生产能力为30，生产的产品输入到v1点，所以给边（x，v1），取C（x，v1）＝30，W（x，v1）＝15.第一季度末销售公司需产品20，所以给边（v1，y），取C（v1，y）＝20，W（v1，y）＝0.又考虑到第一季度生产的产品有部分可能要存储到第二季度末供货，故给边（v1，v2），其容量不妨设为＋∞，同时由所给条件知，单位产品每积压一个季度需付存储费0.2，故有w（v1，v2）＝0.2.

同理给其他有向边及有关参数，我们得网络模型如图6－98所示.显然，本模型的最小代价的最大流的流值必为80.

例6－47　（生产计划问题）　某工厂与客户签订合同，当月起连续3个月每月末向客户提供某型号产品.有关信息如表6－44所示.

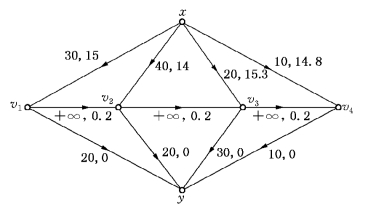
图6－98

表6－44(www.daowen.com)

已知在加班生产时间内，单位产品生产成本比正常生产时高出7.又知单位产品每积压1个月需支付存储费2.在签订合同时，工厂有该产品的库存量5，工厂希望在第3个月的月末完成合同后还能存储该产品10个单位.问工厂应如何安排生产计划，使在满足上述条件的情况下，总的费用为最少？

解　设x1为工厂处于正常生产状态，x2为工厂处于加班生产状态.vj为第j月生产的产品的存储与供货点，x与y分别为源和汇.

由于工厂月初已有库存产品5，它要在1月末才能交货，而单位产品积压1个月的存储费为2，因此给有向边（x，v1），取C（x，v1）＝5，W（x，v1）＝2（本问题假设签订合同前库存的产品的生产成本不核算在本次生产计划的费用内）.

图6－99

不妨设C（x，x1）＝＋∞，C（x，x2）＝＋∞，而W（x，x1）＝0，W（x，x2）＝0.

工厂在当月既可正常生产，又可加班生产，所以给边（x1，v1）和（x2，v1），取C（x1，v1）＝30，C（x2，v1）＝15，W（x1，v1）＝50，W（x2，v1）＝50＋7＝57.

v1点的产品若在1月末未交货，就留存在2月末交货，故给边（v1，v2），取C（v1，v2）＝＋∞，W（v1，v2）＝2.

同理，给出其他有向边和有关参数，得网络模型如图6－99所示.

例6－48　（多阶段存储问题）　某厂部件车间每月生产的部件必须存入备品库，以备以后各月月初组装车间向备品库领取一定数量的部件进行组装使用.由于生产条件的变化，该部件车间在各个月份中生产每个部件所耗费的工时不同.设已知第2至第5个月期间各个月月初组装车间对部件的需求量及各个月部件车间生产每个部件所需的工时如表6－45所给（设1月初该部件库存量为零）.

表6－45

假设备品库的容量限制为9，并要求5月末备品库的部件库存量为零.现考虑1月至5月的总耗费工时最少的逐月生产计划，试建立网络模型.

解　（1）先假定备品库容量没有限制.

设x为源（部件车间），y为汇（组装车间）.又设vk为第k个月月初部件的存储与供货点（即备品库）.1月生产的部件沿边（x，v2）输入v2，在2月初沿边（v2，y）供给组装车间y，剩余的部件可沿边（v2，v3）输入v3，同时，3月生产的部件沿边（x，v3）也输入v3，在3月初沿边（v3，y）供应部件给组装车间，剩余部件沿边（v3，v4）输入v4，依此类推，即得网络图6－100.在图6－100中，取C（x，vk）＝＋∞，W（x，vk）＝dk－1；C（vk，y）＝bk，W（vk，y）＝0；C（vk，vk＋1）＝＋∞，W（vk，vk＋1）＝0.

图6－100

（2）现假定备品库容量有限制，也即顶点vk有容量约束.

显然顶点有容量约束的网络可以化为仅有边的容量约束的网络，具体方法是：

把具有容量约束的顶点v拆为两个顶点v′和v″，同时从v′到v″给有向边（v′，v″），该边的容量即为顶点v的容量，并且原来所有以v为终点的有向边现都改为以v′作为终点，原来以v为起点所有有向边现都改为以v″作为起点，同时这些边的容量都不变.

按此方法，我们将图6－100中的顶点vk拆成两个顶点uk及tk，取C（uk，tk）＝9，即得图6－101，运用最小代价的最大流算法求解，即可得到最优生产计划.

图6－101

例6－49　（生产计划问题）　工厂甲和乙皆生产产品A和B.该两个工厂对产品A和B的工时定额分别定为1和2（工时／件）.表6－46和表6－47给出有关信息.试制订最优生产计划，以使总成本最低.

表6－46

表6－47

解　产品的需要量之单位为件数，而工厂的生产能力的单位为工时，两者单位不统一.为建立网络模型，我们将单位统一为工时.于是，产品需求量（工时）＝需求件数×定额工时，我们得表6－48.

相应地，每件产品的生产成本化为产品每工时成本，每月每件产品的存储费化为每工时的存储费，我们得表6－49.

表6－48

表6－49

建立网络模型如图6－102，其中顶点和参数为

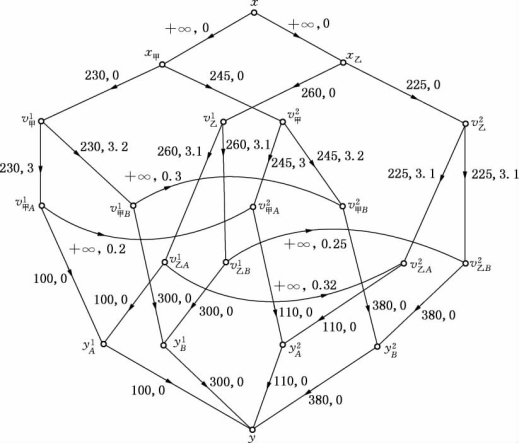
图6－102