对于给定的带代价的网络N＝（V，E，C，W，x，y），定理6－9给我们指出了如何在N中寻求流值为λ的最小代价流的两种方法：

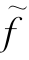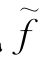方法之一是先在N中任取一个流值为λ的流f（可利用本章§6.8的算法），在其Nf中寻找一个负回路Q.若Q不存在，则f即为所求的最小代价流；否则取δ＝C′（Q），作f关于Q，δ的修改流.视为新的f，再在新的Nf中寻找一个负回路.这样反复迭代，直到找到最小代价流为止.

方法之二是在N中任取一个流值小于λ的最小代价流f（例如，取f为零流），在其Nf中寻求一条x至y的最短路径P，取δ＝min｛C′（P），λ－Valf｝，作f关于P，δ的修改流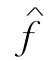，为流值是Valf＋δ的最小代价流.视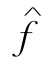为新的流f，重复上述步骤继续进行迭代，直至找到所求的最小代价流.

下面我们给出这两个算法.

求流值为λ的最小代价流算法一：

①在N中任取一个流值为λ的流f.

②作Nf＝（Vf，Ef，C′，W′，x，y）.

③在Nf中是否存在一个负回路Q？

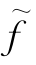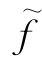若是，则取δ＝C′（Q），作f关于Q，δ的修改流，取f＝，转步骤②；

若否，则f即为所求的最小代价流，算法终止.

求流值为λ的最小代价流算法二：

①取初始流f为零流.

②Valf＝λ？

若是，则f即为N中流值为λ的最小代价流，算法终止；

若否，则作Nf＝（Vf，Ef，C′，W′，x，y）.

③Nf中是否存在一条x至y的路径？

若是，则求Nf中一条x至y的最短路径P.取δ＝min｛C′（P），λ－Valf｝，作f基于P，δ的修改流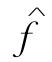，Val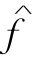＝Valf＋δ.取f＝，转步骤②；

若否，则N中不存在流值为λ的流，f为N中最小代价的最大流，算法终止.

如果我们要求N上的最小代价的最大流，则在应用上述算法时取λ＝＋∞即可.

例6－40　（最优分配问题）　设有x1，x2和x33辆卡车，需指派到y1，y2和y33个不同的目的地，各种指派的运送成本见表6－39，试求能使总成本最低的最优指派.

表6－39

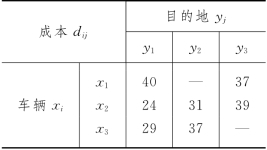
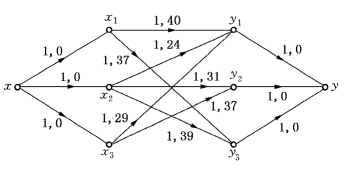
解　建立网络模型如图6－82，边旁参数为C（e），W（e）.

由于一辆车只能派往一个目的地，一个目的地仅需分配一辆车，故图6－82中各边的容量都为1.因为x及y都为虚设的点，故W（x，xi）及W（yj，y）都为零，W（xi，yj）由表6－39中相应成本dij给出.由于车辆x1不能派至目的地y2，车辆x3不能派至目的地y3，故图6－82中顶点x1至顶点y2及顶点x3至顶点y3无有向边.

第一步，给初始流为零流，如图6－83所示（边旁参数为C（e），f（e））.

作它的伴随f的增流网络Nf，如图6－84所示（边旁参数为C′（e），W′（e））.在图6－84中，x至y的最短路径P＝xx2y1y（用双线表示），取δ＝C′（P）＝min｛C′（e）｜e∈P｝＝1.作f关于P，δ的修改流，如图6－85所示.

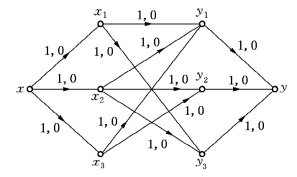
图6－83

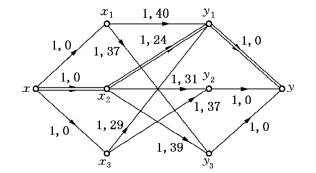
图6－84

第二步，作图6－85的伴随f的增流网络Nf，如图6－86所示，其x至y的最短路径P＝xx3y1x2y2y，取δ＝C′（P）＝1，对图6－85中流进行修改，得f关于P，δ修改流，如图6－87所示.

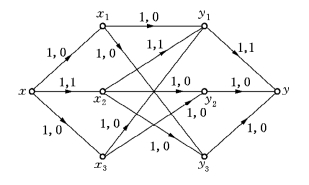
图6－85(www.daowen.com)

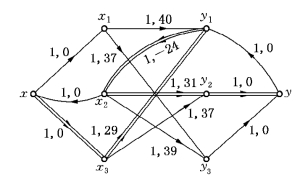
图6－86

第三步，作图6－87的Nf网络，如图6－88所示.在Nf中x至y的最短路径P＝xx1y3y，取δ＝C′（P）＝1，对图6－87中流进行修改，得修改流如图6－89所示.

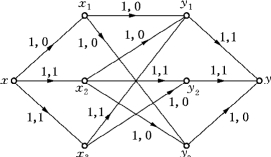
图6－87

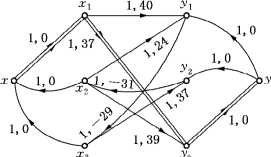
图6－88

显然，图6－89中的流已为最大流.本问题的最优指派如表6－40所给.

表6－40

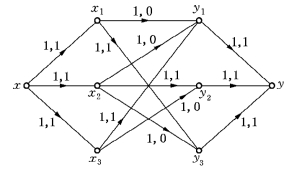
图6－89

例6－41　给出Valf＝11的最小代价流（边旁参数为C（e），f（e），W（e）），如图6－90所示，求Valf＝13的最小代价流.

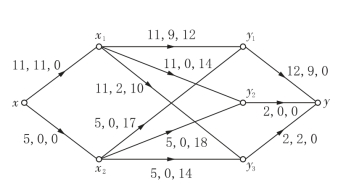
图6－90

图6－91

解　作伴随f的增流网络如图6－91（边旁参数为C′（e），W′（e））所示.

在图6－91中，x至y的最短路径P＝xx2y3x1y1y，

取δ＝min｛C′（P），λ－Valf｝＝2，得到流值13的最小代价流f＊如图6－92所示.

f＊的代价为W（f＊）＝11×12＋2×14＝160.

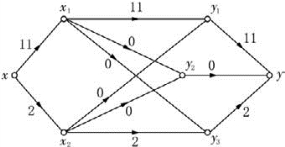
图6－92

例6－42　给出Valf＝11的流如图6－93（边旁参数为C（e），f（e），W（e））所示，判断它是否是最小代价流？若不是，求Valf＝11的最小代价流.

图6－93

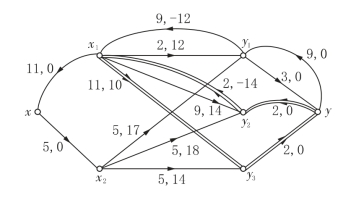
图6－94

解　该网络伴随f的增流网络如图6－94（边旁参数为C′（e），W′（e））所示.

在图6－94中存在负回路x1y3yy2x1，所以它不是最小代价流.取

取δ＝2，在图6－93上进行调整，得Valf＝11的修改流如图6－90所示，即例6－41中所给的初始流，它的伴随f的增流网络如图6－91所示，无负回路，故为最小代价流.