在例6－26图6－55中，若每吨物资从顶点u沿边（u，v）运输到顶点v，运行W（u，v）千米，问如何调运物资，使从x1及x2处运送最多的物资到y1及y2处，而所费总吨千米数最少？这样，我们在建立运输网络时，除了每条边有容量外，又对应了另外一个参数——边的起点到终点的距离.在求最大流时，一方面要考虑每条边的流量符合容量约束和流量守恒条件，另一方面还要考虑流的流程大小.

一般地，给运输网络N＝（V，E，C，x，y），又设非负实数W（u，v）为一个单位的流量从顶点u沿边（u，v）流到顶点v所花的代价（或仍称W（u，v）为边的权，可指距离、时间和费用等各种指标），这样的网络称为带代价的运输网络，或赋权的运输网络，常用N＝（V，E，C，W，x，y）表示.

设f为N上一个流，Valf＝λ，则

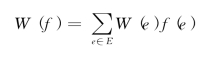
表示N内按照网络流f运送流量λ个单位从源x到汇y所花的代价，称W（f）为流f的代价.

最小代价流——设N为带代价的网络，f＊为N上流，若Valf＊＝λ，且有(www.daowen.com)

则称f＊为N上一个流值为λ的最小代价流.

最小代价的最大流——若λ为N上最大流的流值，则称满足条件（6－36）的流f＊为最小代价的最大流.

本节旨在建立流值为λ的最小代价流和最小代价的最大流算法.当然，这类问题可以归结为我们熟悉的线性规划模型.但考虑到网络模型的直观性、形象性及求解的整数性，本节建立的算法自有它的优点.