例6－35　用最大流算法求解第五章例5－6最优分配问题.

解　显然，车床A1，A2，A3和A4分别加工零件B1，B2，B3和B4，就是一个可行方案，它的全部零件最早完工时间为

表6－32

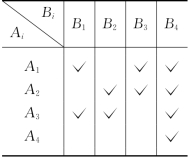
现问：是否存在使完工时间早于5小时的加工方案？加工时间tij小于5小时的加工方式由表6－32给出.

我们建立运输网络模型，用最大流算法对表6－32寻求一种指派方案.

用顶点x1，x2，x3，x4代表4部车床；用顶点y1，y2，y3，y4表示4个零件.若在表6－32中车床可以加工零件yj，则在运输网络中给有向边（xi，yj），其容量为1.又给源x和汇y，有向边（x，xi）及（yj，y）的容量皆为1（这是由于一部车床只能加工一个零件，一个零件只要一部车床加工），得运输网络如图6－69所示.

对网络图6－69用最大流算法求得最大流f＊如图6－70所示，有Valf＊＝4.

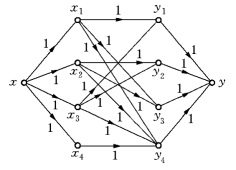
图6－69

图6－70

由图6－70可知：

因此，我们即找到一个全部零件最早完工时间小于5小时的一个加工方案：A1，A2，A3和A4分别加工零件B3，B2，B1和B4，最早完工时间为

现问还可以再提前吗？加工时间tij小于4小时的加工方式由表6－33给出.

对表6－33作相应的运输网络并求得它的最大流如图6－71所示.

表6－33

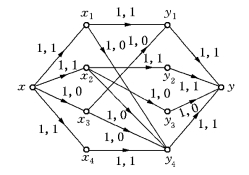
图6－71

图6－71有最大流流值为3，即不存在完工时间早于4小时可行加工计划.所以，使全部零件最早完工的加工方案为

车床A1，A2，A3和A4分别加工零件B3，B2，B1和B4，最早完工时间为4小时.

例6－36　（船只调度问题）　有5批货物，要用船只从发点x1和x2分别运往收点y1，y2和y3.规定的出发日期如表6－34所给，表中x2到y3有两批货物，一批在第一天出发，另一批在第8天出发.又知船只从xi到yj的航行时间（天）如表6－35所给.设每批货物只要一条船装运，且船只在空载和重载时的航行时间相同.问如何编制航行计划，以最少的船只完成这5批货物的运输任务？

表6－34

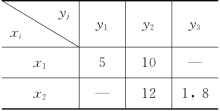
表6－35

(www.daowen.com)

解　设5项运输任务分别为A1，A2，A3，A4和A5，它们的开船时间aj分别为5，10，12，1和8；它们的任务完成时间bi（为船只到达目的地时间，卸货时间不计）分别为7，13，13，3和10.船只在完成任务Ai后接着去执行任务Aj时，它所需要的船只转移时间tij由表6－36给出.例如，t32＝3是船只在完成任务A3（x2→y2）后去执行任务A2（x1→y2）时，它从y2运行到x1所需的转移时间.

表6－36

若船只在完成任务Ai后去执行任务Aj（用Ai→Aj表示），则必须有bi＋tij≤aj，于是，可选的船只调度运输方式由表6－37给出.

类似于例6－34，也把表6－37看成一个指派问题：用顶点u1，u4和u5与表6－37中的行A1，A4和A5相对应；用顶点v1，v2，v3和v5与表6－37中的列A1，A2，A3和A5相对应；若表6－37中允许Ai→Aj，则给有向边（ui，vj），即得运输网络并得其最大流如图6－72所示.

表6－37

图6－72

图6－72的最大流流值为3，且有

因此，任务A1完成后，船只可去执行任务A2；任务A4完成后，船只可去执行任务A5；任务A5完成后，船只可去执行任务A3.从而，5项任务只需2条船：一条船执行任务A1和A2，从x1驶往y1运送一批货物，再开回x1运送第二批货物驶往y2；另一条船依次执行任务A4，A5和A3，从x2运送第四批货物到y3，返回x2运送第五批货物到y3，再返回x2运送第三批货物到y2.

例6－37　（调运计划问题）　某运输系统下属4个发点v1，v2，v3和v4，分别有80，20，80及60个空集装箱急需调运到收点t，其运输线路如图6－73所示（每次运输集装箱只能从一条有向边（u，v）的起点u输送到该边的终点v后，再由发点v作安排），边旁容量为沿该边每次输送该类型集装箱的最大输送能力.从发点到收点所需单位时间如表6－38所给.现每隔一个单位时间各发点可向关联的点发送一次空集装箱，问应如何制订调运计划，使在5个单位时间内有最多的空集装箱调运到收点t？

表6－38

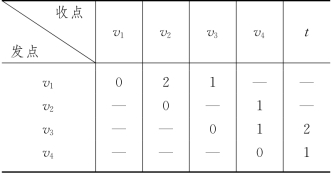
图6－73

解　我们建立运输网络.令x为源，y为汇.

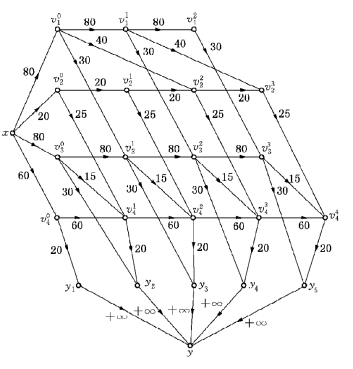
图6－74

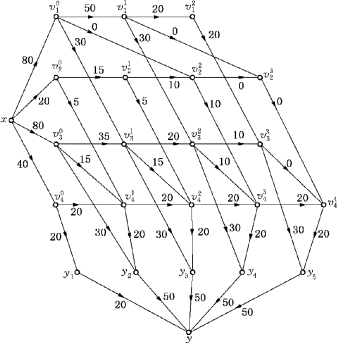
图6－75

在从发点u到收点v的物资输送中，常常会遇到这样一类问题：u点至v点的物资运量至多为C（u，v），至少为b（u，v），即物资流量不但有容量上界约束，而且有容量下界约束.为此，我们有必要来讨论容量有下界的运输网络的最大流算法.

若对运输网络N＝（V，E，C，x，y），又给一个容量参数：任e∈E，有非负整数b（e）：b（e）≤C（e），则称N＝（V，E，C，b，x，y）为有界容量运输网络（这里，对e∈E，b（e）不全为零）.对e∈E，称b（e）为边e的下界容量，称C（e）为边e的上界容量.

有界容量运输网络N上的网络流f（E上非负整数函数）应满足约束：

①b（e）≤f（e）≤C（e），e∈E，

②f＋（v）＝f－（v），v∈I.

对于有界容量运输网络，已经建立了最大流算法，有兴趣的读者可以看阅本书第一版中的“有界容量运输网络及最大流”这一节内容.