【摘要】:图6-68即当(i,j)∈R时,约简矩阵中第i行第j列的零元素被选为独立零,带上括号.我们由集合I和J给定约简矩阵的最少覆盖线:当i∈I时,对矩阵第i行给行覆盖线,当j∈J时,对矩阵第j列给列覆盖线.由于Valf*=C(S,),对约简矩阵按此方法选定的独立零个数与覆盖线数是相等的.例6-34对矩阵(5-57)、矩阵(5-60)用上述方法分别选取最多个数独立零和最少覆盖线.解约简矩阵(5-57)

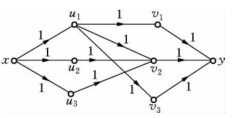
图6-68
即当(i,j)∈R时,约简矩阵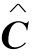 中第i行第j列的零元素被选为独立零,带上括号.
中第i行第j列的零元素被选为独立零,带上括号.
我们由集合I和J给定约简矩阵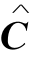 的最少覆盖线:当i∈I时,对矩阵第i行给行覆盖线,当j∈J时,对矩阵第j列给列覆盖线.
的最少覆盖线:当i∈I时,对矩阵第i行给行覆盖线,当j∈J时,对矩阵第j列给列覆盖线.
由于Valf*=C(S,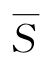 ),对约简矩阵按此方法选定的独立零个数与覆盖线数是相等的.
),对约简矩阵按此方法选定的独立零个数与覆盖线数是相等的.
例6-34 对矩阵(5-57)、矩阵(5-60)用上述方法分别选取最多个数独立零和最少覆盖线.
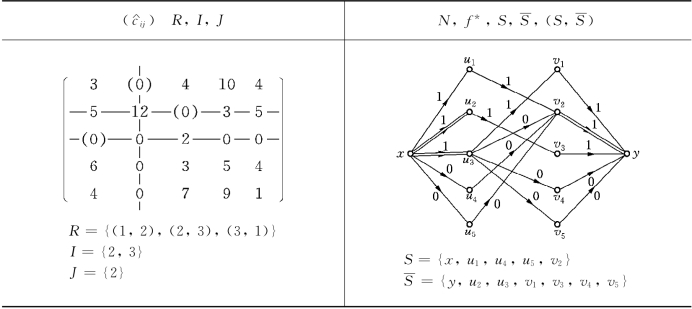
解 约简矩阵(5-57)的最多个数独立零和最少覆盖线的选取如表6-30所示.
表6-30
 (https://www.daowen.com)
(https://www.daowen.com)
在表6-30中,有向边旁的参数为最大流f*的流量f*(e).由于N中容量C(e)≡1,故表中均不再标出容量C(e).N中双线边表示最小割(S,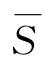 )中的边.由于f*(u1,v2)=f*(u2,v3)=f*(u3,v1)=1,所以有
)中的边.由于f*(u1,v2)=f*(u2,v3)=f*(u3,v1)=1,所以有
![]()
于是在矩阵![]() 取为独立零.同时,
取为独立零.同时,![]() 所以I={2,3},J={2},在
所以I={2,3},J={2},在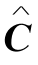 中第2行、第3行和第2列给覆盖线.
中第2行、第3行和第2列给覆盖线.
约简矩阵(5-60)的最多个数独立零和最少覆盖线的选取如表6-31所示.
表6-31
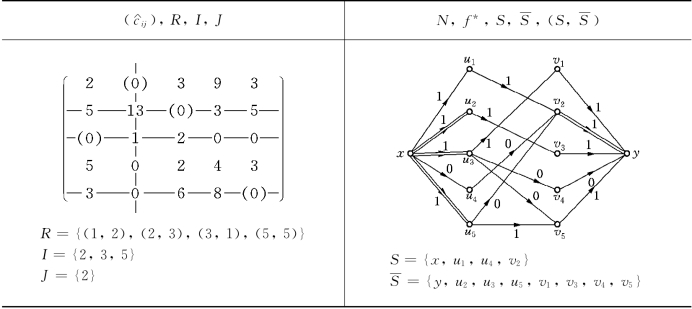
这里我们指出:由于独立零不可能被两次覆盖,所以在由矩阵(5-57)变换为矩阵(5-60)时,矩阵(5-57)中的独立零在矩阵(5-60)中仍为零元素.因此对表6-31所示的网络N求最大流时,可取初始流f为
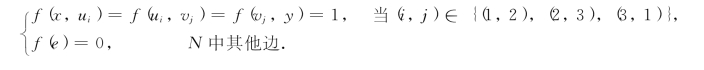
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章








