现在我们关心的问题是，当网络N给定后，如何求得它的一个最大流.

定理6－8为我们提供了寻求运输网络中最大流的一个方法.若给网络N上一个初始流（例如零流），我们判别一下N中有无f增流链：若无f增流链，则f即为最大流；若有f增流链Q，则可得f基于Q的修改流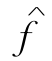，有

再将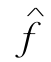视为f，继续迭代.

但是，到此算法还不能说已经建立成功了，因为如何寻求f的增流链这个问题还没有解决.故下面我们先讨论寻求f增流链的方法，然后建立求最大流的算法.我们采用标号的方法来寻求x至y的f增流链.

若f为网络N的一个流，N中满足下列条件的树T称为以x为根的f不饱和树：

①x∈V（T）；

②任v∈V（T），v≠x，T内有唯一的一条初等链Q＝x…v为f不饱和链，l（Q）＞0.

每个点v∈V（T），都按下述方法给以标记：

若T中x至v的初等链为Qv＝x…uv：

①如果（u，v）为N中边，则给v以标号（u，＋，l（v）），其中第一个标号u表明在链Qv中u为v的紧前顶点；第二个标号表明（u，v）在Qv中为前向边；第三个标号l（v）＝l（Qv）（l（Qv）由式（6－23）给出）.显然，有

②如果（v，u）为N中边，则给v以标号（u，－，l（v）），其中第一个标号u表明在链Qv中u为v的紧前顶点，第二个标号表明（v，u）在Qv中为后向边，第三个标号l（v）＝l（Qv）（l（Qv）由式（6－23）给出）.显然，此时有

例如，图6－63为图6－61的一棵f不饱和树.

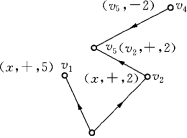
图6－63

我们通过以x为根的f不饱和树T的不断“生长”以及“标记法”来探寻N中f增流链.

初始时，先给x以标号（0，＋，∞）.

一般地，若已得以x为根的f不饱和树T（如图6－63），T中每个顶点都有标号，而yV（T）.可将S＝V（T）中点分成两部分：一部分点已查视过，即已生长了枝的点（例如图6－63中的点x，v2和v5），或判定不能生长枝的点（如图6－63中的点v1）.另一部分点未查视过（如图6－63中的点v4）.我们将T中全部未查视过的点记为A（A为有顺序的集合，先标记的点排在前.本算法的特点为：先标记的点先查视，即先生长枝）.

我们查视A中第一个顶点u能否生长枝？关心下列边：

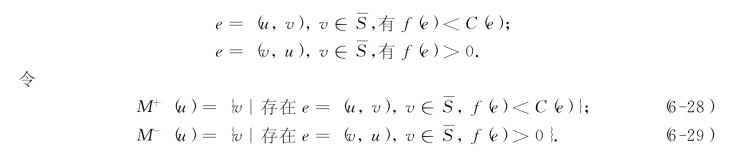
若M＋（u）及M－（u）都为空集，则u点不能生长枝，u点查视完毕，将点u从A中取出.若M＋（u）或M－（u）非空，则将M＋（u）中所有的点v及有向边e＝（u，v）都生长在点u上而成为T的枝；将M－（u）中所有的点v及有向边e＝（v，u）都生长在点u上而成为T的枝.同时，对这些M＋（u）及M－（u）中的点都按我们在上面介绍过的方法给以标号.至此，点u查视完毕，从A中删去.而M＋（u）及M－（u）中的点v按标号前后顺序先后进入A，此时，S∪M＋（u）∪M－（u）成为新的点集S.

倘若u在生长过程中得到边（u，y），则我们求得了x至y的f增流链Qy.我们用逆向追踪法来求f增流链Qy：首先根据点y的标号（u，＋，l（y）），可得Qy中y的紧前顶点u，再根据点u的标号，依次逆向追踪，直至回溯到点x，即可得一条f增流链Qy（由Qy中各点标号的第二部分知链中各边是为前向边还是后向边），且l（y）＝l（Qy）.

若y未进入T，重复上述步骤继续运算.

若T不能再生长（即A＝∅，T中点已全部查视完毕），而y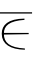V（T），则N中无增流链，f即为最大流，算法即可终止.此时，S＝V（T）为全部已标号的点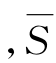为全部未标号的点，可知S即为定理6－8（1）充分性证明中的顶点集合S，于是，（S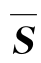，）即为最小割.所以我们说，最大流算法不仅可求得网络N的一个最大流，同时也可求得一个最小割.

为了运算上的方便，我们可将T的生长过程列成表格形式.例如对图6－61，寻找f增流链的过程可列成表6－26（表的第一行为查视某个顶点能否生长枝，第二、三行为被生长的顶点及其标号）.

表6－26

对表6－26的运算过程我们作如下说明：

（1）给x以标号（0，＋，∞），x置入S和A中.查视x：可知M＋（x）＝｛v1，v2｝，M－（x）＝∅.给v1和v2分别以标号（x，＋，l（v1））和（x，＋，l（v2）），其中

其他以此类推.最后，我们运用逆向追踪法，由表6－29得到一条x至y的f不饱和链

基于Qy的修改流f如图6－62所示.

下面我们给出求N中流值为指定值λ的流f的算法（若要求N的最大流，则只要在这一算法中将事先给定的数值λ取为＋∞即可）：

①取N的一个初始流f（例如零流），计算Valf.(www.daowen.com)

②Valf＝λ？

若是，则f即为所求之流，算法终止；

若否，则给x以标号l（x）＝＋∞，S＝｛x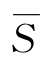｝，＝V－S，A＝｛x｝.

③A＝∅？

若是，则N中无f增流链，f即为最大流，算法终止；

若否，则取A中第一元素u，作

（M＋（u）中点按标号的先后给以顺序）.按式（6－29）取M－（u），转步骤⑤.

若运用上述算法求N的最大流，则算法终止时的顶点集合S与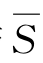对应的割（S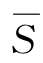，），即为最小割.

例6－32　求运输网络图6－64的最大流及最小割.

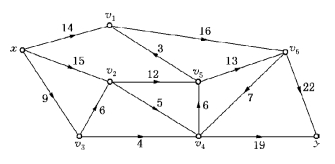
图6－64

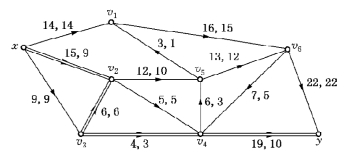
图6－65

解　第一步，给初始流f如图6－65所示.对其寻找f增流链，标号过程如表6－27所示.

表6－27

由表6－27得N的f增流链Qy＝xv2v3v4y（在图6－65中用双线示之），l（Qy）＝l（y）＝1.Qy中边（x，v2），（v3，v4）和（v4，y）为前向边，边（v3，v2）为后向边.得基于Qy的修改流如图6－66所示.

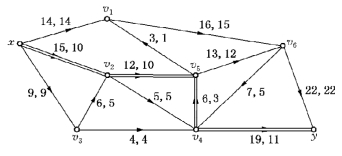
图6－66

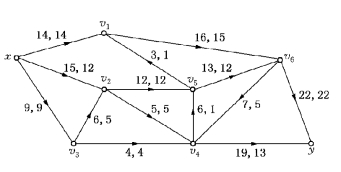
图6－67

第二步，对图6－66寻找f增流链，标号过程如表6－28所示.

表6－28

由表6－28得f增流链Qy＝xv2v5v4y（在图6－66中用双线示之）.得基于Qy的修改流如图6－67所示.

表6－29

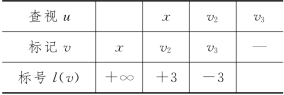
第三步　对图6－67寻找f增流链，标号过程如表6－29所示.

由表6－29可知，图6－67中不存在f增流链，故图6－67中流f即为最大流f＊，有

由表6－29知，已标号的点集S＝｛x，v2，v3｝，未标号的点集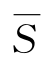＝｛v1，v4，v5，v6，y｝，故最小割

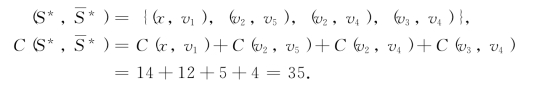
可见，最小割的容量的大小影响最大流的流值.因此，为提高图6－67中最大流的流值，就必须提高最小割（S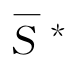＊，）中边的容量.另一方面，一旦最小割中边的容量被降低，则最大流的流值也同时降低.