“一个邮递员每次送信，从邮局出发，必须至少一次地走过他负责投递的范围的每一条街道，待完成任务后仍回到邮局.问他如何选择一条投递路线，使他所走的路程最短？”这个问题是由我国管梅谷同志在1962年首先提出的，因此称为中国邮路问题.

若邮递员管辖的街道图视为无向图G＝（V，E），任e＝〔vi，vj〕∈E，W（e）＝W（vi，vj）＝wij为街道e的长度，则中国邮路问题也就是：

在图G中寻找一条闭链Q＊，使这条闭链Q＊的总长度最短，即

若图G为欧拉图，则我们求G的欧拉环游，它即为最佳投递线路Q＊.

但是，在一般情况下，图G不是欧拉图，它具有偶数个奇阶顶点.此时任一条包含G全部边的闭链必然有一部分边要重复出现，也即邮递员要完成投递任务，必然有部分街道要重复走.邮递员在他的管辖区内走的路程的长短，就取决于重复走的街道的长短.

设Q为一条包含G的全部边的闭链，其中部分边重复出现，我们作相应的图GQ：

若边e＝〔u，v〕在Q中出现k＋1次，则我们就在图G中添加k条〔u，v〕边e1，e2，…，ek（称为添加边），且令每条添加边的权和原来边的权相等.于是，GQ没有奇阶顶点，GQ成为欧拉图，Q就是GQ中的欧拉环游.

例如，在图6－46中取

其中e10，e9，e8各重复一次.

我们即得相应的图GQ，如图6－47所示.

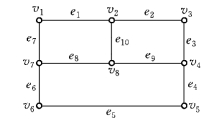
图6－46

图6－47

若Q1及Q2为两条投递线路，则W（Q1）与W（Q2）之差就等于各相应添加边权和的差.从而，要找最短邮递线路Q＊，就只要找出一组添加边的集合F，使它具有下面两个性质：

（1）把它添加到图G上后，得到的新图GQ没有奇阶顶点.

（2）添加边的权和最小.

我们把具有性质（1）的一组添加边F称为一个可行解；具有性质（2）的可行解称为最优解.如前面介绍过的各种迭代算法一样，我们先寻找初始可行解，然后按最优性判别准则检查这个可行解是不是最优解，不是，就把这个可行解调整成另一个更好些的可行解，再检查新的可行解是否为最优解，直至找到最优解为止.

下面给出最优解的判别准则.

定理6－6　若添加边集合F为一个可行解，则F为最优解的充分必要条件为

（1）F中无平行边.

（2）若C为G的任一回路，则该回路的具有添加边的边集C1的总长度

下面我们结合例题来进一步讲解中国邮路问题的算法步骤.

例6－26　求图6－48所示投递街道图的最短投递线路.

解　（1）寻求初始可行解.设无向图G的奇阶顶点为2q个，将这2q个奇阶顶点随意分成q对.因为G是连通图，故每一对奇阶顶点之间必有一条初等链，我们把q条初等链中的边作为添加边添加到G中而得图GQ.这组添加边就是一个可行解.

如图6－48所示，有8个奇阶顶点：v2，v3，v5，v7，v8，v10，v11和v12.将它们分成4对：v3与v10，v2与v5，v11与v8，v12与v7.

在图6－49中，对这4对奇阶顶点分别取链为v3v2v1v10，v2v3v4v5，v11v8和v12v7，把这4条链的全部边作为添加边集合F而得到一个可行解，相应的GQ如图6－49所示.此时

图6－48

(www.daowen.com)

图6－49

（2）调整可行解.

①检查可行解F是否符合定理6－6条件（1）.若某两个顶点u与v间有F中两条或两条以上平行边，则从F及GQ中删去偶数条u与v间的添加边，图GQ显然仍无奇阶顶点，故剩下的添加边集合F还是一个可行解，但W（F）却下降了.

如在图6－49中，顶点v2与v3间有两条添加边，故可删去它们而得图6－50.此时

②判别可行解F是否为最优解.

对G的任一回路C，检查定理6－6条件（2）是否成立.

可知，如果G中某个回路C中边集C1在F中有相应的添加边，那么我们若作一次调整，在F中删去C1的边所相应的添加边，换成C－C1的边所相应的添加边，这时图GQ仍无奇阶顶点，F仍为可行解.故若对某个回路C，有W（C1）＞W（C），我们如上所说作一次调整，那么W（F）就必然下降了.

若对G的任一回路，定理6－6条件（2）都成立，则F即为最优解.我们对GQ求欧拉环游，即得最短投递线路.

如在图6－50中，G的回路v1v2v3v12v7v8v11v10v1的权为20，而相应添加边的权为11，大于回路权的一半.因此，作一次调整而得图6－51，此时，W（F）＝14.

图6－50

图6－51

在图6－51中，G的回路v3v4v5v12v3的权为10，而相应添加边的权为7，大于回路权的一半，作一次调整而得图6－52，此时，W（F）＝10.

对图6－52，定理6－6的条件（2）对G的任一回路都成立，可知F为最优解.求图6－52的欧拉环游，最短投递路线如图6－53虚线边所示，其长度为52.

图6－52

图6－53

我们将求最短投递线路的奇偶点图上作业法归纳如下：

①把G的2q个奇阶顶点分成q对，每对顶点间取一条初等链，该q条初等链中边的全体取为初始可行解F.

②F中是否有平行边？

若是，则删除偶数条平行边，转步骤③.

若否，则转步骤③.

③对任一回路C和式（6－16）所给C1，W（C1）≤是否成立？

若是，则F即为最优解.在GQ中运用欧拉环游算法求得欧拉环游Q，即为最短投递线路.

若否，则将C1在F中相应的添加边换成C2＝C－C1相应的添加边，转步骤③.

奇偶点图上作业法在实际运用中已作出了许多贡献.它不仅可以提高邮递员的工作效率，而且对于街道清扫路线、纺织工看车路线、仓库员巡视货物路线等类似问题的研究，都有实际意义.

但奇偶点图上作业法还不够理想，用起来不够方便，主要困难在于步骤③，需要对G中每个回路作检查，而这不是很容易的.像图6－48这样十分简单的图，却也有22个回路.那么比图6－48稍为复杂一点的图，回路可以多到几百个，检查起来就不胜其烦了.同时，该方法在调整过程中，某一个回路调整合格后，还可能会影响本来已合格的回路，使其成为不合格的，这样更增加了计算量.埃德蒙（Edmods）和约翰逊（Johnson）于1973年提出一种比较有效的方法，有兴趣的读者可参考Math Programming，5（1973），88－124.