例6－24　某一料场货物堆放如图6－37.每晚有个值班小组沿巡视道路进行巡视检查.问应如何设置两个休息站及如何确定一条以两个休息站为起终点的巡视路线，使每条应巡视的道路恰走过一次？

我们将图6－37画成图6－38的形式.于是，该问题成为在图6－38中寻找一条开链，每条边在链中恰出现一次.这是一个图的一笔画问题，而起点和终点不相同.

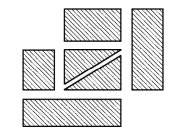
图6－37

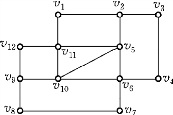
图6－38

对于例6－2的七座桥问题，我们已指出过，它也是一个图的一笔画问题，只是该问题要求起点和终点必须相同.

所以从应用出发，我们有必要从数学上认识一笔画问题.

下面我们先介绍一些有关术语.

欧拉链——若无向图G为连通图，Q为G的一条链，G的每一条边在Q中恰出现一次，则称Q为欧拉（Euler）链.

欧拉环游——闭的欧拉链称为欧拉环游.

欧拉图——若无向图G含有一条欧拉环游，则称图G为欧拉图.

顶点阶数——无向图G中与顶点v关联的边数称为顶点的阶数，记作δ（v）.

若δ（v）为偶数，则称v为偶阶顶点；若δ（v）为奇数，则称v为奇阶顶点.

例如在图6－38中，有

定理6－5　（1）连通无向图G为欧拉图的充要条件为G中无奇阶顶点.

（2）连通无向图G含有欧拉开链的充要条件为G中奇阶顶点个数为2.

定理6－5反映了无向图的一笔画性质.事实是：一个能一笔画成的图，必须有一个作为起点的顶点和一个作为终点的顶点.图中其余顶点v都只能是“过路”的顶点，若有“到达”就必有“离去”，至于到达v点多少次数没有关系，只要离去v点的次数和到达的次数相同，它便是一个“过路”顶点.由于规定一笔画中不准有重复的边，故每次到达和离去都选用不同的边.因而顶点必然与偶数条边相关联，也就是说，一个“过路”的顶点，必然是阶数为偶数的顶点，只有起点和终点才可以允许为奇阶顶点.从而，本定理为我们提供了一个识别一个图能否一笔画出的极为简单的办法：如果连通无向图G无奇阶顶点，则该图能一笔画成，且起点和终点相同；如果连通无向图G有2个奇阶顶点，则该图也能一笔画成，但起点和终点不相同.

例如7座桥问题图6－4有4个奇阶顶点，所以不能一笔画成.而图6－38有2个奇阶顶点，故可以一笔画成，而在两个奇阶顶点处可以设置休息站.

为给出算法，我们对无向图G给如下运算：

图6－39(www.daowen.com)

图6－40

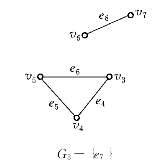
图6－41

由此得出结论：在延长链

时，在连通图中取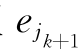时，除非Gk中仅有一条与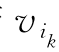关联的边，否则总不取Gk的割边为.

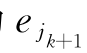下面我们给出求欧拉环游的弗鲁瑞（Fleury）算法：

①任取欧拉图G中一个顶点，E＝∅，k＝0.

②k＝m？

若是，则算法终止，Qk即为所求的欧拉环游.

若否，则在Gk＝G－E中选取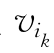的关联边为：除非Gk中仅有一条边与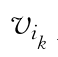关联，否则总不取Gk的割边为k＝k＋1，转步骤②.

我们可以把画出欧拉图的欧拉环游的方法总结成口诀：画一条边，原有图中抹一条边，余下的图形不断掉.

例6－25　求图6－42的欧拉环游.

解　在进行一笔画时，先把要画的那个图画在左边，而在右边进行一笔画.每当在右边画一条边时，就把左边图上相应的一条边抹去，只要抹去的这条边不使左边的图成为分离图即可.这样一直画下去，最后一定会把整个图不重复地一笔画出，即得欧拉环游.图6－43和图6－44表示求图6－42一笔画的过程，图6－45为图6－42的欧拉环游.

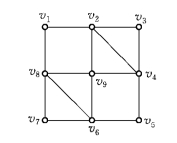
图6－42

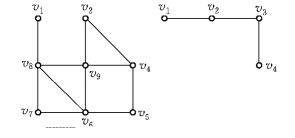
图6－43

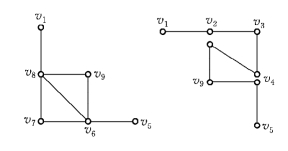
图6－44

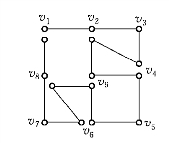
图6－45