由定理6-1知,生成树应无回路且边数为n-1.克鲁斯卡(Kruskal)算法根据“在无回路的条件下优先选取权小的边”这一原则,从G的m条边中逐个挑选出n-1条边来.运算过程中,我们记被挑选到的边的集合为E1.
首先,我们把G的m条边按权的递增顺序进行排列,不妨设为
![]()
然后,依次逐条检查,以“选入E1不使E1的导出子图有回路”为条件来挑选进入E1的边.
初始时,选e1进入E1.
设当前检查到ek.如果E1∪{ek}的导出子图没有回路,就将ek选进E1,否则就不选取ek,而继续检查ek+1.当E1中含有n-1条边时,G关于E1的导出子图即为我们所求的最小生成树.
为判别G关于E1∪{e}的导出子图是否含有回路,我们可采用对V中顶点给以标号的方法来解决.
可知E1的导出子图G1虽然无回路,但不一定是树.G1可能是个分离图,由数个连通的子图组成,每个连通子图是树.由此出发,我们对V中顶点采取如下的标号方法:
初始时,对任vj∈V,取vj的标号l(vj)=j.当e1=〔u,v〕置入E1时,则取l(u)=l(v)=min{l(u),l(v)},其余顶点标号不变.
第k步时,若e=〔s,t〕刚被选入E1.当e加入到E1∪{e}的导出子图的某个连通子图时,则这个连通子图中顶点标号为max{l(s),l(t)}者,改其顶点标号为min{l(s),l(t)}.
这样规定的标号方法,具有这样的特性:两个顶点当且仅当属于G1的某个连通子图时,两个顶点具有相同标号(该两顶点间有初等链相连接).换言之,G1中两个没有初等链连接的顶点的标号一定不相同.
于是,在运算过程的某一步检查e=〔s,t〕是否要被选进E1时,我们只要检查l(s)是否与l(t)相等.
若l(s)=l(t),说明s与t已在当前E1的导出子图G1的某个连通子图中,s与t之间有初等链.这样的e=〔s,t〕,一旦选入E1,则E1∪{e}的导出子图中就有回路.所以l(s)=l(t)的e不可以被选入E1.
若l(s)≠l(t),则e=〔s,t〕应被选入E1.
下面,我们给出克鲁斯卡算法:
①将G的m条边按权的递增顺序进行排列.现不妨设(https://www.daowen.com)

④E1中边数|E1|=n-1?
若是,则G关于E1的导出子图即为最小生成树T*,算法终止.
若否,则取k=k+1,转步骤②.
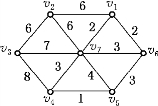
图6-35
例6-23 求图6-35的一棵最小生成树.
解 整个运算过程由图6-36(a)~(g)给出.这些图中顶点旁带方框的数字表示该顶点的标号,双线边表示当前已在E1内的边.最小生成树T*由图6-36(g)中双线边表示.可知
![]()
现在我们结合图6-36对顶点的标号过程,来解释算法中的步骤③.
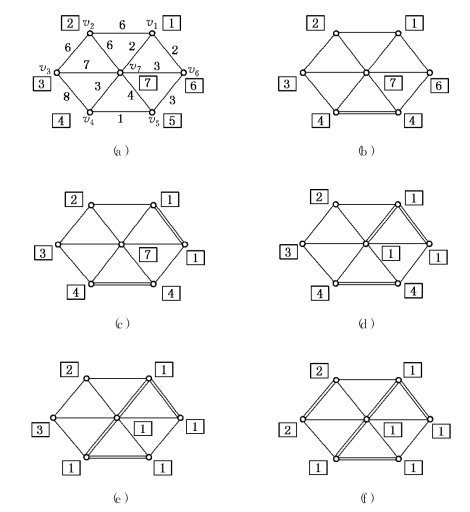
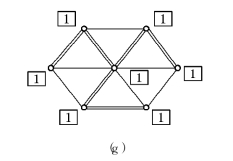
图6-36
例如,对图6-36(d)来说,此时E1={[v4,v5],[v1,v6],[v1,v7]},E1的导出子图分成两个连通子图,它们顶点标号分别为4和1.下一步我们将选边e=[v7,v4]进入E1,现在
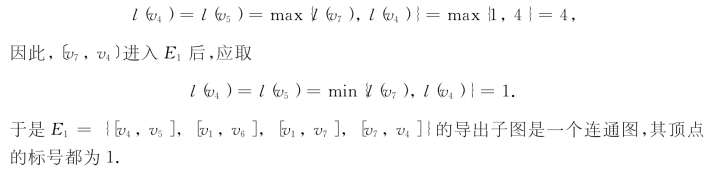
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






