现给非负赋权有向图D＝（V，E），其中V＝｛v1，…，vn｝，任e∈E，有权W（e）≥0.

在很多实际问题中，由于客观条件的限制，对图D（不妨设为完备图），我们除了关心顶点v1至顶点v的最短路径外，还对顶点v1至顶点v的第k短路径发生兴趣.

第k短路径——若P1，P2，…，Pk为顶点v1至顶点v的k条路径，W（P1）≤W（P2）≤…≤W（Pk），现P为顶点v1至顶点v的任一条路径P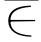｛P1，…，Pk｝，且W（P）≥W（Pk），则称Pk为顶点v1至顶点v的第k短路径.

例6－20　某工厂研制新产品，研究工作已近尾声.但要将新产品正式投产，还需4个阶段工作，每个阶段的工作可在不同水准上完成，所需时间W由表6－22给出.有10个单位费用可供这些阶段使用.在不同水准上的费用由表6－23给出.现问：在预算的限制下，每个阶段工作按哪一水准进行才能使完成4个阶段工作的总时间最小？

表6－22

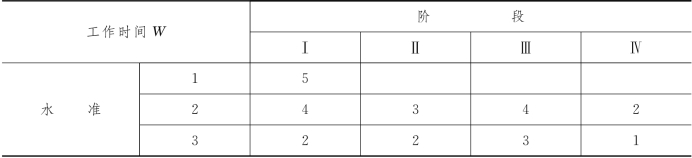
表6－23

解　对此问题我们建立网络模型如图6－30所示，其中顶点v2，v3，v4分别表示在水准1、水准2、水准3条件下进行阶段Ⅰ的工作，顶点v5，v6分别表示在水准2和水准3条件下进行阶段Ⅱ工作，顶点v7和v8分别表示在水准2和水准3条件下进行阶段Ⅲ工作，顶点v9和v10分别表示在水准2和水准3条件下进行阶段Ⅳ工作.有向边（vi，vj）旁的权wij表示在某水准下进行某阶段工作所需时间.

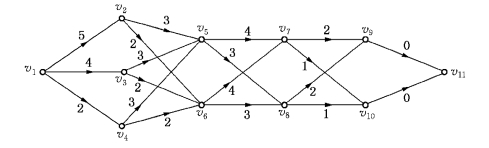
图6－30

显然，顶点v1至顶点v11的一条路径表示一个具体的方案，其长度为采取该方案时完成4个阶段工作所需时间.

可知图6－30中顶点v1至v11的最短路径为

它的长度为8，相应的方案为4个阶段工作都在水准3的条件下完成，因此其费用(www.daowen.com)

显然它超过了可提供的费用10.

该例子说明，我们有必要研究第k短路径问题.

为建立求第k短路径的算法，下面我们引进一些定义及记号.

偏移——若有路径

表6－24

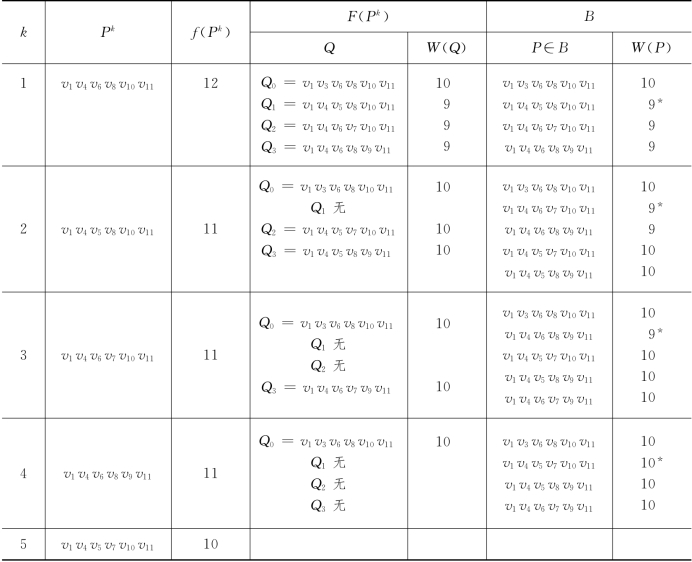
在表6－24中第k步对P∈B，W（P）打＊者，则在第k＋1步时该P即为Pk＋1.

由表6－24求得P5＝v1v4v5v7v10v11，故本问题的最佳方案为

阶段Ⅰ工作取水准3，阶段Ⅱ工作取水准2，阶段Ⅲ工作取水准2，阶段Ⅳ工作取水准3.4个阶段工作总时间为10，费用为10.