一些初看似乎和最短路径问题不相干的问题，有时也可以构建成网络模型而用最短路径算法来求解.

例6－12　（设备更新问题）　某工厂使用一种设备，每年年初该厂需对该设备的更新与否作出决策.若购置新设备，就要支付一定的购置费用；若继续使用旧设备，则需支付一定的维修费.设备使用的年数越长，每年所需的维修费用就越大.现若该厂在第一年年初购置了一台新设备，问在5年内应如何制定一个设备更新计划，以便在使用一台这种设备时“新设备购置费和旧设备维修费”的总费用最小？若已知该设备在5年内购买的价格如表6－8所给，设备使用不同年数的维修费如表6－9所列.

表6－8

表6－9

解　这种设备的更新方案是很多的.最显然的：每年年初购买一台设备更换旧的，故5年内购置费为11＋11＋12＋12＋13＝59；工厂每年对这台设备的维修费为5＋5＋5＋5＋5＝25，所以总费用为59＋25＝84.

又如另一个方案：在第一年、第三年和第五年购买新设备，购置费为

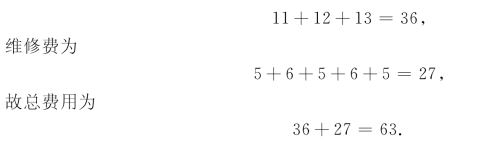
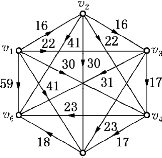
图6－22

若年限在5年以上，要为这类问题穷举出所有可能采取的方案，费时很大.现在，我们建立数学模型，用最短路径算法来求解.

建立网络模型D如图6－22所示：

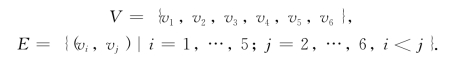
在此，v1，v2，…，v5相当于第1，2，…，5年的年初，v6相当于第5年年末.E中有向边（vi，vj）相当于第i年年初购买一台设备一直用到第j－1年年末.

显然，对于每一种可能的设备更新方案，在此图中都有相应的一条从v1至v6的路径.例如，路径v1v3v5v6相当于第1，3，5年年初购买新设备这一方案.

E中边的权按如下法则给出：

W（vi，vj）＝第i年设备的购置费＋（j－i）年里的设备维修费＝ai＋（b1＋b2＋…＋bj－i）.

例如，边（v2，v5）表示第2年年初购买一台新设备，使用至第4年年底，故它的购置费为a2＝11，维修费为b1＋b2＋b3＝5＋6＋8＝19.于是，边（v2，v5）上的权w25＝30.

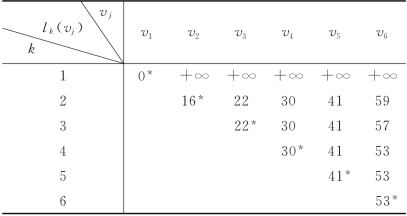
这样，制订一个最优的设备更新方案的问题就等价于寻求D中v1至v6的最短路径问题.应用迪奇斯特算法求解，运算表格如表6－10所示.

最短路径为v1v3v6，即第1，3年购买新设备；或者最短路径为v1v4v6，即第1，4年购买新设备.5年的总费用都为53.

若制订更新计划的期限分成60个时段（例如一个月或一个季度为一个时段），那么，就有260≈1.15×1018个购买策略可供选取.若一台计算机每秒钟可计算106种策略，要将全部策略估算一遍的时间就要36 599年，但构建网络模型用最短路径算法来求解仅需一分钟左右.

表6－10

例6－13　（多阶段存储问题）　某工厂生产产品所需的原材料分3个阶段进货.根据供货条件，每次进货量q只能从5，7和10个单位中选一个方案，其运费Q（q）分别为120，138和160个单位.第i阶段对原材料的需求量为ai个单位：a1＝7，a2＝8，a3＝9.已知第一阶段初工厂仓库已存储该原材料3个单位.仓库对该原材料最大库存量允许为6个单位.本阶段进货在本阶段就供应生产的原材料不必进仓库.每阶段末仓库存储的原材料需付存储费，每单位原材料的存储费为1个单位.现要求第3阶段末库存的原材料至少为1个单位.

问在保证生产需求的条件下，每阶段进货采用何种方案，能使运费和存储费总和最少？

解　我们作iOs平面直角坐标系.点（i，s）表示第i阶段末仓库对该原材料的库存量为s.

(www.daowen.com)

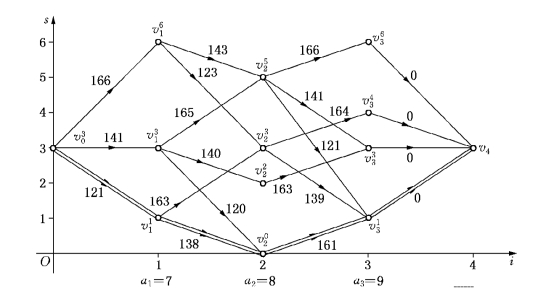
图6－23

下面我们来讨论图6－23的顶点和边是如何设立的.

总费用为420.

例6－14　（选址问题）　现准备在v1，v2，…，v7等7个居民点中设置一个售票处，各点之间的距离由图6－24给出.问售票处设在哪个居民点，可使最大服务距离为最小？若要设置两个售票处，问应设在哪两个居民点？

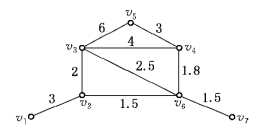
图6－24

解　我们求出任意两个顶点vi与vj之间的最短路径长度d（vi，vj）＝dij，得矩阵d＝（dij）如下：

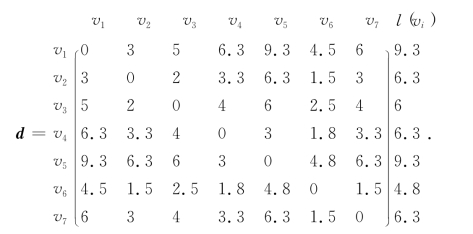
我们依次对顶点vi求l（vi）（i＝1，…，7）：

称l（vi）为vi的最大服务距离，并将（l（v1），…，l（v7））T置于矩阵d的最右列.

l（vi）的实际意义是：如果我们把售票处设在vi，那么售票处与最远的服务对象间的距离是l（vi）.这样，最大服务距离越小的点，设置为售票处就越好.现在

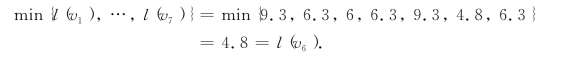
故若设置一个售票处，则设在居民点v6处较好.

下面考虑设置两个售票处.

假若设在v3和v6.那么对点v1来说，居民可以到v3处购票，也可以到v6处购票.由矩阵d知d13＝5及d16＝4.5，这样，v1处的居民自然选择到v6处购票，其服务距离为4.5.我们依次找出居民点v2，…，v7的服务距离，将有关信息列成表6－11.

表6－11

从表6－11中可看出，当售票处设在v3和v6时，最大服务距离为

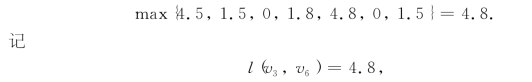
我们求任意一对顶点vi和vj的最大服务距离l（vi，vj），并将它们列成矩阵L＝（l（vi，vj））：

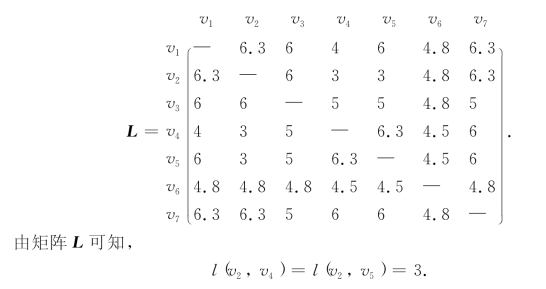
在诸l（vi，vj）中为最小，故售票处拟设置在v2及v4或设置在v2及v5.