给有向图D＝（V，E），V＝｛v1，…，vn｝，且任e∈E，有权W（e）≥0.我们称D为非负赋权图.狄克斯特拉（Dijkstra）在1959年提出的算法，是目前公认的求最短路径的较好的算法之一.该算法可求非负赋权图D中顶点v1至各顶点vj（1≤j≤n）的最短路径及其长度.

图6－18

我们用顶点标号方法，遵循“让d1j小的顶点vj优先生长的”原则，逐步生长这棵以v1为根的方向树T.

解　对图6－18（b）所示树T的生长标号过程，我们列成运算表格如表6－3所示.

表6－3

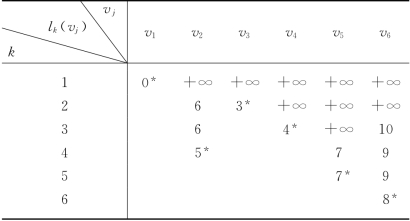
第一步，k＝1，l（v1）＝0，其他顶点的标号l（vj）＝＋∞，取l1（v＊）＝l1（v1）＝将v＊＝v1（在运算表中在l1（v＊）右上角标以＊号，以后类同）置入树T中.在算法中，我们把已经求到最短路径长度的顶点置于集合A＝V（T）中，

(www.daowen.com)

例6－9　求图6－19中v1至v8的最短路径及其长度.

图6－19

表6－4

求顶点v1至vj的最短路径的另一方法是：结合赋权图来查视哪些顶点的永久性标号之差恰等于关联边的权，那么把有关的顶点串联起来，即得v1至vj的最短路径.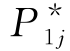

例如例6－9，结合图6－19来分析，我们还能得到另一条v1至v8的最短路径

继续逆向追踪，即得v1至v8的两条最短路径.

我们还须指出，本算法虽然是用来求非负赋权有向图的最短路径的，但它对于非负赋权无向图的最短路径问题同样适用.只需把连接顶点u和v的无向边e＝［u，v］改为有向（u，v）和（v，u），且它们的权W（u，v）和W（v，u）都为W（e）.