在生产实践、运输管理和工程建设的很多活动中，诸如物资的运输线路、各种工艺路线的安排、厂区及货场的布局、管道线网的铺设及设备的更新等等问题，都与寻找一个“图的最短路径”问题密切相关，它是网络规划中的一个最基本的问题.

假若，现给有向图D＝（V，E），V＝｛v1，…，vn｝.设图D的每条边e＝（vi，vj）都与一个实数W（e）＝W（vi，vj）＝wij对应，W（e）称为边e的权，图D称为赋权图.

这里所说的“权”，是指与边有关的数量指标.根据实际问题的需要，可以赋予它不同的含义，例如表示距离、时间和费用等等.以后我们讨论的图都为赋权图，俗称网络.

若P为D中u至v的路径，称W（P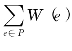）＝为路径P的长度.

若P＊为D中u至v的路径，且有

则称P＊为D中u至v的最短路径.(www.daowen.com)

我们的目的就是在图D中寻找u至v的最短路径并求出其长度.

不妨假定D为完备图.不然，若u至v有平行边，则保留权最小的边；若u至v不存在有向边，则可设一条u至v的有向边e，其权W（e）＝＋∞（于是，如果原来的图D中u不能到达v，现在修改的图中u就可到达v，但是，u至v的最短路径长度为＋∞）.

显然，若u至v有最短路径（其长度＜＋∞），则最短路径可能不止一条.

下面我们给出最短路径问题的两个算法.