如何把图的有关信息输入和存储到电子计算机里去呢？我们知道，图的最本质的内容是顶点与边或者顶点与顶点之间的关联关系，我们不难用矩阵来表示这种关联关系.

给无向图G＝（V，E），其中V＝｛v1，…，vn｝，E＝｛e1，…，em｝.若用矩阵的行标号i对应图G的顶点下标，用列标号j对应图G的边的下标，可构造一个n×m矩阵A（G）＝（aij）n×m与图G对应，其中

称矩阵A为图G的关联矩阵，它描写了无向图G的顶点与边的关联情况.

若矩阵的行标号i和列标号j都对应图G顶点下标，则可以构造一个n×n矩阵B（G）＝（bij）n×n与图G对应，其中

并称矩阵B为图G的邻接矩阵，它描写了图G的顶点间的邻接情况.

例6－6　写出图6－6的关联矩阵和邻接矩阵.

解　在矩阵A外的左边一列标出图G诸顶点，在矩阵的上方一行标出图G的诸边，得图6－6的关联矩阵如下：

显见，矩阵A中第i行的各元素之和为与vi关联的边数，而A的任一列元素之和恒为2.

在矩阵B外的左边一列及上方一行标出图G的诸顶点，得图6－6的邻接矩阵：

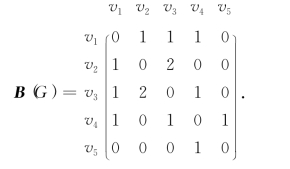(www.daowen.com)

邻接矩阵主对角线上的元素都为零，它是一个对称矩阵.显然，若图G为简单图，则B（G）的元素bij取值不是0就是1.

给有向图D＝（V，E），其中V＝｛v1，…，vn｝，E＝｛e1，…，em｝，可构造它的n×m关联矩阵A（D）＝（aij）n×m，其中

图D的邻接矩阵B（D）＝（bij）n×n的元素bij为

例6－7　写出图6－11的关联矩阵和邻接矩阵.

解　图6－11的关联矩阵A（D）如下：

图6－11的邻接矩阵B（D）如下：

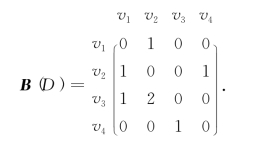
显见，对有向图D，A（D）的第j列各元素之和为零，而B（D）的第i行元素之和为以vi为起点的有向边的边数，B（D）第j列元素之和为以vj为终点的有向边的边数.

当V和E中元素的次序固定后，图与矩阵A或B是一一对应的，故而关联矩阵或邻接矩阵是描述图的另一种方式.