有向图——设V是一个有n个顶点的非空集合:V={v1,…,vn};E是一个有m条有向边的集合:E={e1,…,em},则称V和E这两个集合组成了一个有向图,记作有向图D=(V,E).
若e∈E,u为有向边e的起点,v为有向边e的终点,则记e=(u,v).
例6-5 给有向图D=(V,E),其中V={v1,v2,v3,v4},E={e1,…,e7},边与顶点的关联情况如表6-2所示.
表6-2

对表6-2作其几何图,如图6-11所示.
类似于无向图,有向图D也有下列术语.
平行边——不同的有向边e与e′的起点与终点都相同,则称边e与e′为有向图D的平行边.如图6-11中的边e3与e4.
孤立点——V中不与E中任一条边关联的点称为D的孤立点.例如在图6-13中,v1为孤立点.
简单图——无平行边的有向图称为简单图.
完备图——图中任两个顶点u与v之间,恰有两条有向边(u,v),及(v,u),则称该有向图D为完备图.
基本图——把有向图D的每条边除去定向就得到一个相应的无向图G,称G为D的基本图.称D为G的定向图.
子图——设D=(V,E)和D1=(V1,E1)都是有向图,且V1⊆V,E1⊆E,则称D1为D的子图,并记为D1⊆D.
导出子图——若V1⊂V,E1={e|e=(u,v)∈E,u,v∈V1},则称有向图D1=(V1,E1)为有向图D中关于V1的导出子图.例如,图6-12是图6-11关于V1={v2,v3,v4}的导出子图.
导出生成子图——若D1=(V1,E1)是有向图D关于V1的导出子图,则图(V,E1)称为D关于V1的导出生成子图,记为D(V1)=(V,E1).例如,图6-13是图6-11关于V1={v2,v3,v4}的导出生成子图.
同构图——如果有向图D1=(V1,E1)和有向图D2=(V2,E2)的顶点集合V1和V2以及边集E1和E2之间在保持关联性质的条件下一一对应,则称图D1和D2为同构图(对无向图也有同样定义).
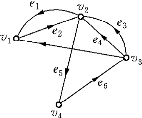
图6-11

图6-12(www.daowen.com)
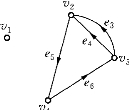
图6-13
例如图6-14和图6-15初看是不一样的,但如果令ui与vi(i=1,…,4)对应,(ui,uj)与(vi,vj)相对应,由于对应边与对应顶点关联,所以这两个图就是同构的.
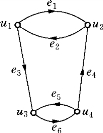
图6-14
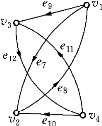
图6-15
形象地说,若图的顶点可以任意挪动位置,而边是完全弹性的,只要在不拉断的条件下,一个图可以变为另一个图,那么,这两个图就是同构的.
由于同构的图被认为是相同的,这就给我们在网络规划中建立网络模型带来许多方便.当我们用几何图来构建网络模型时,点的位置可以任意布置,边的长短曲直也可任意,故而我们尽量设计那种反映问题清晰、简练的几何图.
链——若Q是有向图D的基本图G中的一条链,则Q就称为D的一条链.
初等链——若Q是有向图D的基本图G中的一条初等链,则Q就称为D的一条初等链.
路——若Q是有向图D的基本图G中一条链,且有![]() (s=1,…,k),则称Q为D的
(s=1,…,k),则称Q为D的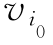 至
至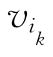 的单向路,简称为路.
的单向路,简称为路.
路径——若有向图D的路Q中每个顶点都不相同,则称Q为D的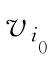 至
至 的单向路径,简称路径,并称
的单向路径,简称路径,并称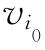 可达
可达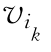 .
.
回路——若有向图D的单向路径Q的第一个顶点与最后一个顶点相同,则称Q为D的单向回路,简称回路.
若e为链、路、路径、回路Q中的边,则可写为e∈Q.
在简单图中,可用顶点序列来表示相应的链、路、路径.
例如,在图6-11中,有
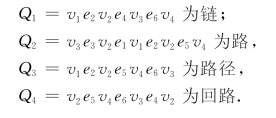
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






