无向图——设V是一个有n个顶点的非空集合：V＝｛v1，…，vn｝；E是一个有m条无向边的集合：E＝｛e1，…，em｝，则称V和E这两个集合组成了一个无向图，记作无向图G＝（V，E）.

E中任一条边e若连接顶点u和v，则记为e＝［u，v］（或［v，u］），并称u与v为无向边的两个端点；边e与顶点u及v相关联，顶点u与顶点v相邻.

对于图G，有时为说明问题，V与E也可写作V（G）及E（G）.

给出图G＝（V，E），我们可以作出它的几何图.在以后的讨论中，我们往往直接对几何图进行讨论.

例6－4　给无向图G＝（V，E），其中V＝｛v1，…，v5｝，E＝｛e1，…，e7｝，边与顶点的关联情况由表6－1给出.

表6－1

根据表6－1，可作其几何图，如图6－6所示.

在作几何图时，仅要求表示出顶点、边以及它们之间的关联状况，而对于顶点位置的布置以及边的曲直、长短都没有任何规定.从而，同一图G＝（V，E），可以有许多不同的几何图.如例6－4所给的图，也可表示成图6－7.在图6－7中，边在非端点处可能出现交点，但这种交点不是顶点.

基于无向图G的结构特点，我们给出下列术语.

平行边——若两条不同的边e与e′具有相同的端点，则称e与e′为G的平行边.如图6－6中的边e3与e2即为平行边.

简单图——若图G无平行边，则称图G为简单图.如图6－8.

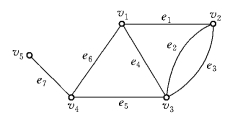
图6－6

图6－7

图6－8

完备图——若图G中任两个顶点之间恰有一条边相关联，则称图G为完备图.如图6－8所示.(www.daowen.com)

子图——设G＝（V，E），G1＝（V1，E1）都是图，且V1⊆V，E1⊆E，则称图G1为图G的子图，并记为图G1⊆G.

生成子图——若G1⊆G，且V1＝V，则称图G1为图G的生成子图.

导出子图——设图G＝（V，E），非空边集E1⊂E，如果G中与E1中诸边相关联的顶点全体记为V1，则子图G1＝（V1，E1）称为图G的由E1导出的子图.记G（E1）＝（V1，E1）＝G1.

例如图6－9给出的图G1是图6－6所给图的子图；若取E1＝｛e1，e7｝，则图6－9所示图G1是图6－6所示图G关于E1的导出子图；图6－10所示图G2是图6－6所示图G的生成子图.

图6－9

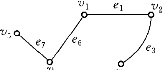
图6－10

链——无向图G中一个由顶点和边交错而成的非空有限序列：

初等链——若开链Q中诸顶点皆不相同，则称Q为一条初等链.

回路——若一个闭链Q，除了第一个顶点和最后一个顶点相同外，没有相同的顶点和相同的边，则该闭链Q称为回路.

例如，在图6－6所示图中，

连通图——若图G中任意两顶点u和v之间存在一条链（称u与v在G内连通），则称图G为连通图.否则，称为分离图.

例如，图6－6所示图为连通图，图6－9所示图为分离图.

割边——若G为连通图，将G中边e取走后所得图为分离图，则称e为图G的割边.

例如，图6－10为连通图，e6为图6－10所给图G2的割边.