我们先通过几个直观的例子，来感性地认识什么是图.

例6－1　图6－1所画的是某地区的铁路交通图.显然，对于一位只关心自甲站到乙站需经过哪些站的旅客来说，图6－2比图6－1更为清晰.但这两个图有很大的差异：图6－2中不仅略去了对了解铁路交通毫无关系的河流、湖泊，而且铁路线的长短、曲直及铁路上各站间的相对位置都有了改变.不过，我们可以看到，图6－1中各站间的连通关系在图6－2中丝毫没有改变.

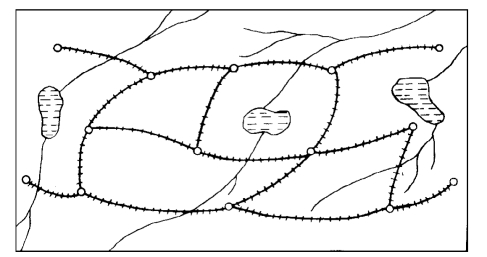
图6－1

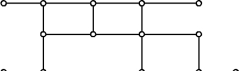
图6－2

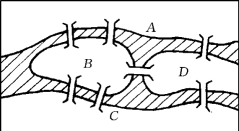
图6－3

例6－2 18世纪的东欧有个哥尼斯堡城，流贯全城的普雷格尔河两岸和河中两个小岛彼此间有7座桥相通，如图6－3所示.(www.daowen.com)

这个城镇里的居民当时热衷于这样一个问题：从岸上任一地方开始，能否通过每座桥一次且仅仅一次就能回到原地.1736年欧拉发表了图论方面的第一篇论文，将此难题化成了一个数学问题：用点表示两岸或小岛，用点之间的联线表示陆地之间的桥，这样就得到了图6－4所示的一个图.从而，问题就变为：在这个图中，是否可能从某一点出发只经过各条边一次且仅仅一次而又回到出发点，即一笔画问题.在图6－4中可见，两岸和岛的大小形状及桥的长短曲直都被置之一旁，但陆地间的关联情况却依然得到保持.

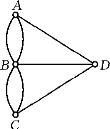
图6－4

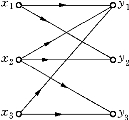
图6－5

例6－3　若发点x1可运送物资到收点y1和y2；发点x2可运送物资到收点y1，y2和y3；发点x3可运送物资到收点y1和y3.现用点表示发点或收点，带方向的边表示物资运送方向，即得图6－5.

由这几个例子，我们可以得到一个结论：一个图由一个表示具体事物的点（图论中称为顶点）的集合和表示事物之间联系的边的集合组成.

根据边的带方向与否，图又可分为有向图及无向图，下面我们分别对它们介绍有关的概念.