建立最优分配问题的数学模型，即是给出费用矩阵C＝（cij）n×n（cij≥0，i，j＝1，…，n），下面我们来看几个例子.

例5－27　n个职工分别从事n项工作，i＃职工从事j＃工作的收益为dij，问如何进行工作分配，使总收益最大？

求最优分配.

解　在最优分配问题中，费用矩阵C是n行n列，为此，我们对本问题所给矩阵添加第五行，其每个元素都为零，得矩阵C：

我们对最优分配问题（C）求解，即可得本问题的最优解.

例5－29　机器A1，A2，A3加工零件B1，B2，B3，B4的费用矩阵为

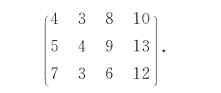
若每台机器至多可加工两个零件，至少需加工一个零件，试建立最优分配问题数学模型.

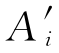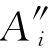解　我们把每台机器Ai拆成两台机器和，它们加工零件Bj的成本是一样的，于是得矩阵

由于上述矩阵行数和列数不相同，我们虚设两个零件B5和B6.考虑到机器Ai（i＝1，2，3）必须加工B1，B2，B3和B4中的一个，所以在取ci5＝ci6＝0（i＝1，3，5）以后，我们取ck5＝ck6＝M（k＝2，4，6）.于是，得最优分配问题的费用矩阵C如下：(www.daowen.com)

例5－30　（铁路列车运行分派问题）　A站与B站之间拟开7对客车，客车运行图如图5－19所示，图中粗实线旁数字表示列车的车次，奇数为下行车（A站至B站），偶数为上行车（B站至A站）.现在要给列车固定乘务组，A站的乘务组换班地点在A站.现在假定，乘务组在对方折返停留的最短时间为2小时.A站的乘务组如服务全部的7对列车，则在B站的折返停留时间如矩阵A（例如，A站的乘务组固定5次车及10次车，则该乘务组在B站的列车折返停留时间由图5－18知为6小时，这是因为5次车9点到达B站，10次车15点离开B站）所示.同样，如果B站的乘务组服务这7对列车，则在A站的折返停留时间如矩阵B所示.现在希望7个乘务组在折返站的总时耗最小，问如何分派任务？

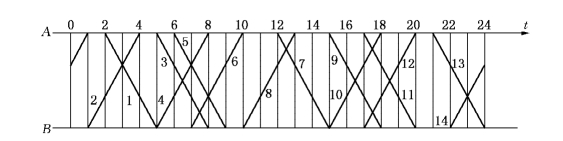
图5－19

解　由矩阵A和B可见，每一对列车的乘务组在折返站的停留时耗与服务的方案有关.例如1次车与6次车这对客车若由A站乘务组服务，则在B站的停留时耗为a16＝2小时；若由B站乘务组服务，则在A站的停留时耗为b16＝16小时.可见1次车与6次车这对客车由A站乘务组服务为好.由此出发，比较矩阵A与矩阵B的每一对元素，取得矩阵C如矩阵（5－63）.在矩阵（5－63）中，元素cij右下角字母A或B表示i次车及j次车这对客车由A站或B站乘务组服务.

我们的问题就成为求解最优分配问题（C）（即解决下行车与上行车的配对问题）.用匈牙利方法求得本问题的最优配对，如表5－49所示（在矩阵（5－63）中打＊记号的数字相应的xij＝1），总时耗为20小时.

表5－49