定理5－1　若对费用矩阵C＝（cij）的第k行或第k列的元素减去同一数值d，则对于分配问题（C）得到一个等价问题

问题是如何寻求这类约简矩阵？下面结合求解例5－26来介绍匈牙利方法的具体步骤.

例5－26　一个“5台机器、5个零件”的最优分配问题的费用矩阵由矩阵（5－56）给出：

步骤③：用最少的覆盖线覆盖约简矩阵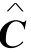中的全部零元素.寻找未覆盖的元素中的最小数ε（它总是一个正数），再进行矩阵变换，其变换规则为

①未覆盖的元素减去ε；

②一次覆盖的元素照旧；

③二次覆盖的元素增加ε.

这样，又得到一个新的约简矩阵），再转步骤②.

例如矩阵（5－57）的最少覆盖线为3，它恰等于矩阵（5－57）的最多独立零的个数，如矩阵（5－57）所示.

我们有下列定理.

定理5－2　在约简矩阵中能选择到的独立零的最多个数，恰等于覆盖矩阵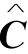中所有零元素的最少覆盖线.

在矩阵（5－58）中，ε＝1，为了说明变换规则的由来，我们分步变换矩阵（5－58）.

对约简矩阵（5－58）中未有覆盖线的行的所有元素都减去ε＝1，得下列矩阵(www.daowen.com)

在上述矩阵（5－59）第2列（在矩阵（5－58）中有列覆盖线）中出现了负数，对该列元素加上ε＝1，得约简矩阵：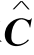

如果直接按变换规则来变换矩阵（5－58），所得结果即为矩阵（5－60）.

由矩阵（5－58）变换为矩阵（5－60）的过程可见：若覆盖矩阵零元素的覆盖线数为m，其中行覆盖线数为m1，列覆盖线数为m2，则此时约简常量为

现在对矩阵（5－58）来说，n＝5，m＝3，ε＝1，故由矩阵（5－58）变换为矩阵（5－60），其约简常量为（5－3）×1＝2.

对矩阵（5－60）重复步骤②：选择的最多独立零与最少覆盖线如矩阵（5－61）：

由于矩阵（5－61）中最多独立零个数4小于5，因此对其重复步骤③，取ε＝2，得矩阵（5－62），此时约简常量（n－m）ε＝（5－4）×2＝2，

在矩阵（5－62）中有5个独立零，于是得本问题的最优分配：

怎样寻找约简矩阵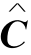中最多独立零与最少覆盖线，现在的运筹学教材都介绍了人工观察法（可见本书第一版相关内容），可是这种人工观察法不能编成计算机程序，意义不大.由于我们练习的例题中的n都较小，最多独立零与最少覆盖线都不难找到，所以本书略去了人工观察法.本书在第六章网络规划§6.8最大流一节中，应用最大流算法可寻找最多独立零与最少覆盖线，感兴趣的读者可参见相关内容.

在手工计算时，如果我们在约简矩阵中选择到的独立零的个数不是最大，那么在选择最少覆盖线时，将出现独立零被覆盖两次（即独立零是两根覆盖线的交叉点），说明运算有差错，必须进行修改.

我们在这里指出，对于最优分配问题模型（5－52），也可以建立分支定界法.如果模型（5－52）的可行域记为K0，该问题记为（K0），我们可以这样来取它的松弛问题：

把问题（K0）的约束条件放宽为一台机器可以加工多个零件，一个零件仅需一台机器加工，其模型为：