我们先通过求解一个具体的实例来分析一下，在用分支定界法求解纯整数规划问题时，如何对活问题进行分支.

例5－19　应用分支定界法求解下列（AIP）：

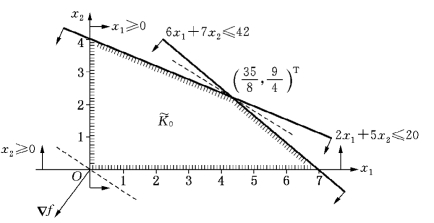
图5－11

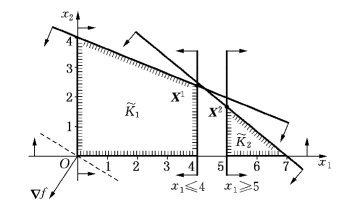
图5－12

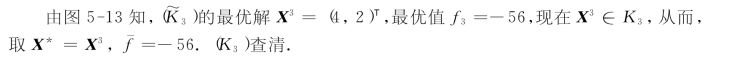
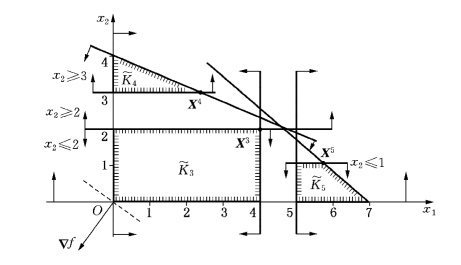
图5－13

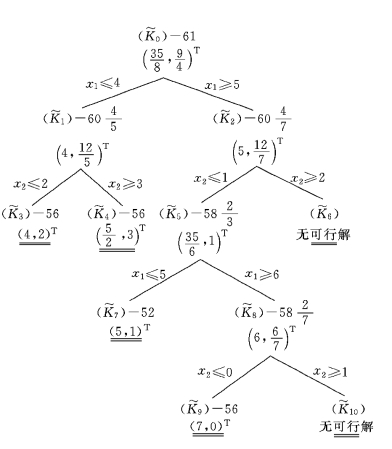
图5－14

表5－33

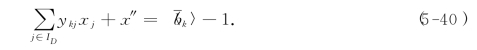
我们将这两个方程加到T（B）上去，即可得到的初始单纯形表，如表5－34和表5－35所示.然后利用对偶单纯形法继续求解.

表5－34

表5－35

表5－36

表5－37

表5－38

(www.daowen.com)

表5－39

表5－40

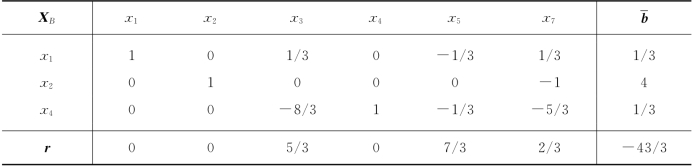
表5－41

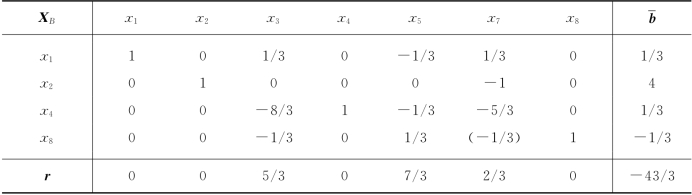
表5－42

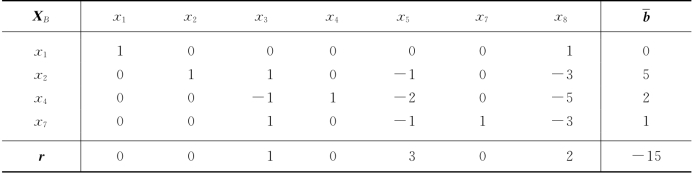
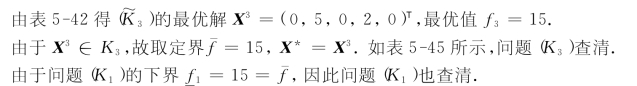
②对求解.将x1≥1附加到表5－40上，按表5－35得表5－43，继续迭代，得表5－44.

表5－43

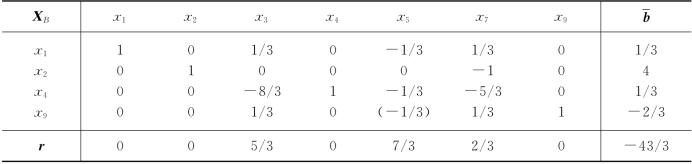
表5－44

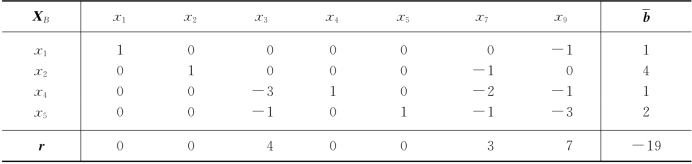
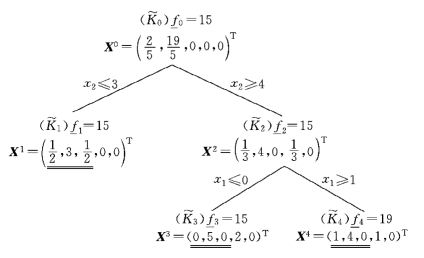
图5－15

表5－45

在归纳（AIP）的分支定界法的算法以前，我们先对若干符号作解释以便理解算法：

L——迭代至某一步时，枚举树中所有问题的下标集合；

E——当前枚举树中已查清的问题和已划分的问题的下标集合；

L－E——当前枚举树中活问题的下标集合；

l——当前枚举树中问题的最大下标；

S——在枚举树中，当前正在划分的问题的下标.

对于混合整数规划（MIP），只要对（AIP）的分支定界法稍作修改，就不难得到（MIP）的分支定界法.

在用分支定界法求解纯整数规划的过程中，我们看到，随着枚举树的不断生长，一些划分变量的上下界在起着变化，且子问题的单纯形表随着划分变量上下界约束条件不断的加入而变得越来越庞大，基本变量个数越来越多.这个问题已经解决，“有界技术”中的“有界变量的对偶单纯形法”，将可以使分支定界法在求解过程中，所有单纯形表的基本变量个数始终保持所给问题中方程AX＝b的个数m，而给计算带来许多方便.感兴趣的读者可以看阅本书第一版中的“有界技术在（AIP）分支定界法中的应用”这一节内容.

怎么加快分支定界法求解的收敛速度，这也是学者一直在探讨的问题，读者可以参阅有关著作中的“分支定界法进一步探讨”，它介绍了割平面法与对偶单纯形法在分支定界法中的进一步应用，对怎么“分支”、怎么“定界”而加快算法收敛进行了讨论.