给定一个混合整数规划(MIP):
![]()
其中N1⊂{1,…,n}.记指标集N2={1,…,n}-N1,(MIP)的可行域记为KMIP.
设B是(MIP)相应的线性规划(LP)的一个基,X是(MIP)的一个可行解,Bk∈N1,则
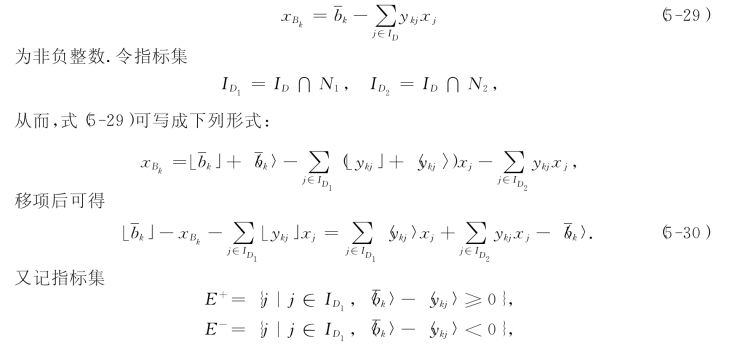

由于式(5-32)和式(5-34)之中恰有一个成立,且两式的左端均是非负的,从而,便得到如下结论:当X为(MIP)的可行解时,必须满足下列约束条件:
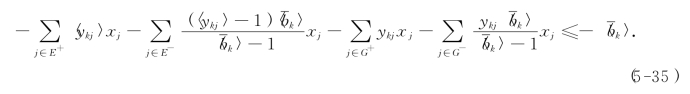
我们称它为柯莫利割.
如果B是(MIP)相应线性规划(LP)的一个最优基,X*为(LP)的基本最优解,且![]() .这时,一定存在一个
.这时,一定存在一个![]() .于是,我们就对原线性规划(LP)增加约束条件(5-35)而得一个新的线性规划.对割平面(5-35)引入松弛变量xn+1,我们可由原来的单纯形表T(B)得到新的(LP)的一张单纯形表,如表5-25所示,然后用对偶单纯形法继续求解.
.于是,我们就对原线性规划(LP)增加约束条件(5-35)而得一个新的线性规划.对割平面(5-35)引入松弛变量xn+1,我们可由原来的单纯形表T(B)得到新的(LP)的一张单纯形表,如表5-25所示,然后用对偶单纯形法继续求解.
表5-25

其中
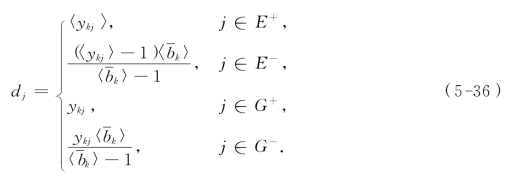
下面我们给出(MIP)的割平面法(假设(MIP)相应的线性规划的可行域非空有界).
①应用单纯形法求解(MIP)相应的线性规划(LP).得(LP)的最优基B、T(B)和基本最优解X*.
②![]() =0对一切Bi∈N1是否都成立?
=0对一切Bi∈N1是否都成立?
若是,则(MIP)中变量在X*中的相应数值即为(MIP)的最优解,算法终止.(https://www.daowen.com)
若否,则取〈![]() 〉=max
〉=max![]() ,将柯莫利割(5-35)作为新的约束条件加入(LP)得到新的(LP),按表5-25从T(B)得到新的单纯形表T(B).
,将柯莫利割(5-35)作为新的约束条件加入(LP)得到新的(LP),按表5-25从T(B)得到新的单纯形表T(B).
③从T(B)出发,应用对偶单纯形法求解,得最优解X*、最优基B和最优表T(B),转步骤②(在用对偶单纯形法求解过程中,若有先前附加在某个柯莫利割(5-35)的松弛变量x′在转轴后由非基本变量再次成为基本变量,则可以从单纯形表中删去x′相应的行和列).
例5-17 应用割平面法求解下列(MIP):
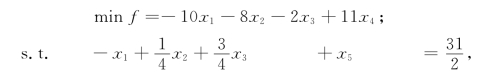
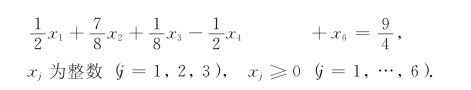
解 应用单纯形法求解相应的(LP),得最优单纯形表,如表5-26所示.现在N1={1,2,3},N2={4,5,6},ID={2,3,4,6},ID1=(2,3),ID2={4,6}.
表5-26


对其引进松弛变量x7,并将该割平面加入(LP),按单纯形表表5-25,从表5-26得单纯形表,如表5-27所示.
表5-27

对表5-27用对偶单纯形法进行一次转轴,得表5-28.
表5-28
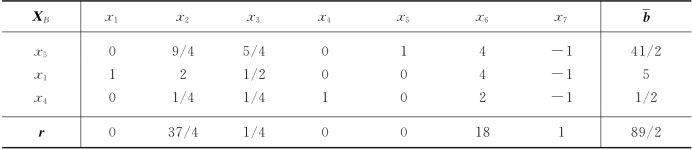
由表5-28,即得(MIP)的最优解:
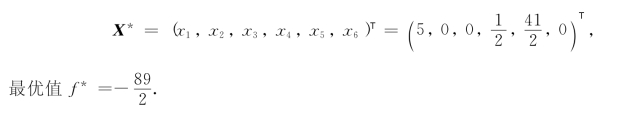
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





