现假设（AIP）相应的（LP）的可行域KLP非空有界，我们给出柯莫利割平面法的算法步骤如下：

①用单纯形算法求解（LP），得基本最优解X＊，B为最优基，T（B）为最优表.

②X＊是否为整数解？

若是，则（AIP）中变量在X＊中的相应数值即为（AIP）的最优解，算法终止.

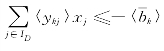若否，则取〈｜1≤i≤m｝，把柯莫利割－作为新的约束条件加入（LP）得到新的（LP），按表5－9从T（B）得到视作新的T（B）.

③从T（B）出发，应用对偶单纯形法求解（LP），得最优解X＊、最优基B和最优表T（B），转步骤②.

按此算法，自然会产生这样的问题：随着柯莫利割的序贯增加，单纯形表会越来越大，基本变量个数会越来越多.此外，也会出现多个基本变量是柯莫利割松弛变量的情况.然而，这种情况完全可以避免.在理论上已经证明，对上述算法我们可作如下补充：在步骤③应用对偶单纯形法求解（LP）的过程中，如果发现转轴后，先前附加在某个柯莫利割的松弛变量x′再次成为基本变量，则可以从单纯形表中删去x′相应的行和列.被x′附加的柯莫利割也从切割可行域KLP的约束条件中删去.这样处理后，迭代过程中的单纯形表至多含有n＋1个基本变量（原问题的n个决策变量和一个柯莫利割的松弛变量），切割（LP）的可行域KLP的柯莫利割至多n＋1－m个.

例5－16　求解下列（AIP）：

解　（AIP）相应的线性规划（LP）的最优单纯形表如表5－15所示.

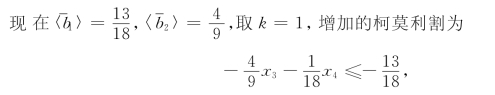
得单纯形表如表5－16所示.

表5－15

表5－16

对表5－16，应用对偶单纯形法进行转轴得表5－17.对表5－17，取k＝3，增加的柯莫利割为

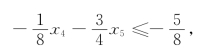
得单纯形表如表5－18所示.

表5－17

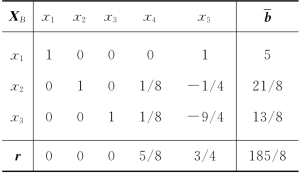
表5－18(www.daowen.com)

将表5－18转轴得表5－19.我们发现，关于第一个柯莫利割－的松弛变量x5再次在表5－19中成为基本变量，故这时可以从表5－19中删去x5相应的行和列（柯莫利割－也被删去），得表5－20.

表5－19

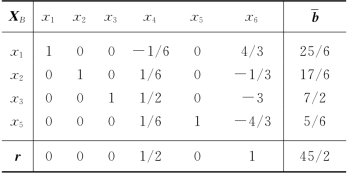
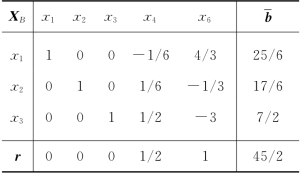
表5－20

对于表5－20，取k＝2，增加的柯莫利割为

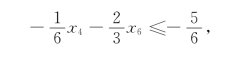
得单纯形表如表5－21所示.对表5－21进行转轴得表5－22.

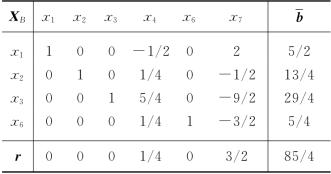
表5－21

表5－22

在表5－22中，柯莫利割－的松弛变量x6再次成为基本变量.故可对表5－22删去x6相应的行和列，并取k＝1，增加柯莫利割得单纯形表如表5－23.对表5－23进行转轴，得表5－24.

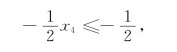
表5－23

表5－24

可见，已得（AIP）的最优解X＊＝（x1，x2，x3，x4）T＝（3，3，6，1）T，最优值f＊＝－21.

从数学上我们可以严格地证明，使用割平面法对KLP经有限次切割后必定能求到（ATP）的最优解.但是，经验证明，如果不考虑（AIP）问题的大小，是不能使用割平面法来解（AIP）的.甚至有些相当小的（AIP）问题在应用割平面法求解时，其收敛速度都相当慢.某些例题向我们表明，约束条件顺序的随意更改都会大大地影响收敛速度.所以一般认为，不能用割平面法单独有效地求解（AIP）.但是，若将割平面法和后面介绍的分支定界法配合使用，一般说来，能收到比较好的效果.