割平面法的关键在于如何寻找适当的切割约束条件，下面我们来讨论这个问题.

我们引进几个记号：

设x为一个实数，则⎿x」表示不超过x的最大整数；「x⏋表示不小于x的最小整数；〈x〉＝x－⎿x」（有〈x〉≥0）.

该条件（5－20）是（AIP）任何一个可行解X必须满足的条件，我们称它为柯莫利（Gomory）割.

假设B是（LP）的最优基，X＊是（LP）关于基B的基本最优解，X＊不是整数解.这时，

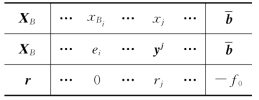
表5－8

这个柯莫利割可以作为我们所需要的切割约束条件，它把X＊从KLP中切割出去.

假设（LP）关于基B和X＊的最优表T（B）如表5－8所示.

我们对柯莫利割（5－21）引进松弛变量xn＋1，得方程：

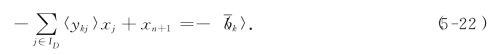
设对（LP）增加柯莫利割（5－22）后所得的新线性规划为（LP1），我们取（LP1）的初始指标集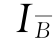＝IB∪｛xn＋1｝（xn＋1作为第m＋1个基本变量，初始基为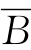），在单纯形表T（B）表5－8中添加xn＋1列和xn＋1行，则我们即得（LP1）的初始单纯形表T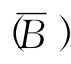如表5－9（由于cn＋1＝0，因此r所在行信息未变）所示.

表5－9

对表5－9，我们用对偶单纯形法继续求解.

例5－15　用割平面法求解例5－13.

解　引进松弛变量x3和x4，将问题化成标准型：

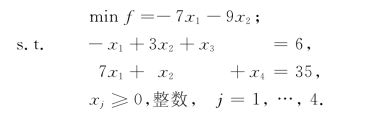
因为松弛变量

所以当x1和x2为整数时，x3和x4也一定是整数.

应用单纯形法求解相应的线性规划（LP），得最优表如表5－10所示.

表5－10

(www.daowen.com)

由表5－10和表5－9，我们得表5－11.

表5－11

对表5－11，我们用对偶单纯形法转轴，得表5－12.

表5－12

对表5－12，取k＝3，得柯莫利割：

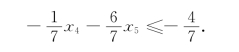
引进松弛变量x6，得

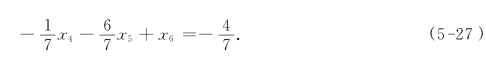
对表5－12增加柯莫利割（5－27），得表5－13.

表5－13

用对偶单纯形法对表5－13进行转轴，得表5－14.

表5－14

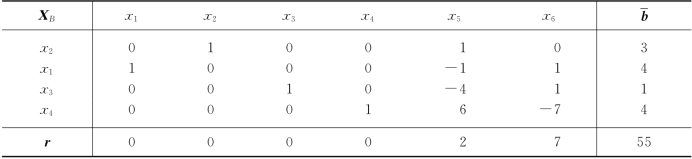
由表5－14可知，我们已得本问题的最优解X＊＝（x1，x2）T＝（4，3）T，最优值f＊＝－55.

如果我们将式（5－23）和式（5－24）代入式（5－26）中，经过整理得

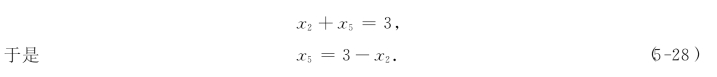
将式（5－24）和式（5－28）代入式（5－27）中，经过整理得：

由于x5≥0和x6≥0，我们便得到例5－13所考虑的两个割平面：