记纯整数规划（AIP）的可行域为KAIP.若将（AIP）中要求变量为整数这个约束去掉，则得到相应的线性规划（LP），记（LP）的可行域为KLP.

割平面法实质上仍然是用解线性规划的方法来求解整数规划问题.其基本思想是：

我们对（LP）求解.若（LP）的最优解X＊是一个整数解（整数向量），那么X＊当然是（AIP）的最优解；若X＊不是整数解，我们设法对原线性规划（LP）增加一个线性约束条件（称它为割平面），把包括X＊在内的不含整数解的一部分集合从（LP）的可行域KLP中切割出去，再求增加了这个约束条件后新的线性规划（LP1）的最优解X＊＊.如果X＊＊是整数解，则X＊＊就是（AIP）的最优解，否则再次增加线性约束条件而重复上述过程.

下面我们来看一个实例.

例5－14　求解下列纯整数规划：

(www.daowen.com)

解　我们用图解法在x1Ox2直角坐标平面内求解相应的线性规划（P）.由图5－6可知，（P）的最优解X1＝（x1，x2）T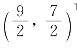＝，它不是整数解.

我们对（P）增加约束条件，例如x2≤3，新的线性规划（P1）的最优解X2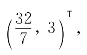＝它仍然不是整数解.我们对（P1）再设法增加新的约束条件，例如x1＋x2≤7，得新的线性规划（P2）.（P2）的最优解X3为（4，3）T，它是整数解，所以它就是整数规划的最优解了.

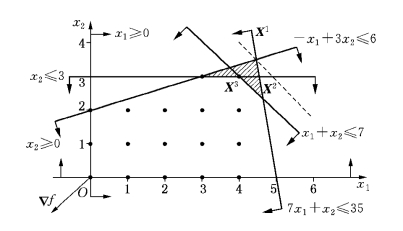
图5－6