人们对整数规划感兴趣,除了有些问题的实际变量必须是整数这个原因外,还因为现实生活中有些问题的解必须满足许多重要的特殊约束条件,或者在建立模型时,必须考虑一些重要的因素,如若不引进附加的整数变量(仅取0或1,称为逻辑变量或0-1变量),那么,要完整地建立模型并把问题说清楚将是十分困难的.下面我们通过一些简单的例题,来介绍建立整数规划模型的一些技巧.
例5-2 (固定费用问题) 工厂准备生产A1,A2,A33种产品.若Aj产品投产,无论产量大与小,都需要一笔固定费用dj(例如装夹具的设计制作费用).而每生产一件产品,其利润为cj,试问固定费用这个因素如何体现在模型中而使总利润最大(其他约束条件暂不列入)?
解 设产品Aj的产量为xj.又设0-1变量
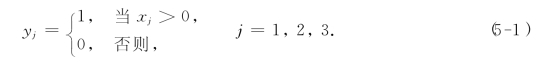
于是,目标函数为
![]()
式(5-1)这个规定可以借助于下列3个约束条件并结合目标函数是求最大值来实现:
![]()
其中M是充分大的正数.
我们可以看到,若xj>0,则要使约束条件xj≤Myj成立,yj就必须等于1,此时,产品Aj的固定费用dj就考虑在目标函数中了.若xj=0,那么yj=0或1都满足约束条件xj≤Myj,但是在最优解中,yj一定等于0.否则,如果yj=1,相应的目标函数值就小于yj=0对应的目标函数值,而我们现在是求max f.因此,引进逻辑变量yj=0,1(j=1,2,3),固定费用就体现在模型中了.
例5-3 (选择性约束条件) 某工厂生产第j种产品的数量为xj,j=1,2,3.其使用的材料在材料甲及乙中选择一种.材料消耗的约束条件分别为
![]()
(其他资源约束未列出),试问这类选择性约束条件如何体现在模型中?
解 引进0-1变量y:

这样,“或此或彼”相互排斥的约束条件就可化成下列两个约束条件:
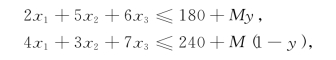
其中M是充分大的正数.
可以看出,当y=0时,第二个约束变成4x1+3x2+7x3≤240+M,由于M是充分大的正数,所以这个约束条件自动满足而不起作用,而第一个约束为2x1+5x2+6x3≤180,这意味着选择材料甲;反之,当y=1时,第二个约束起作用,第一个约束变为2x1+5x2+6x3≤180+M不起作用,这意味着选择材料乙.因此,借助于0-1变量,材料选择的两种可能性就同时包括在一个模型中了.
一般地,假定在某种情况下要在p个约束条件
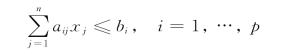
中至少要选择q个约束条件得到满足,那么,我们引进p个0-1变量yi,则选择性的约束条件问题就化为
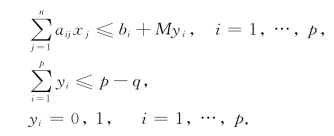
例5-4 (可行域描述问题) 如何把图5-2中的阴影部分所表示的可行域用联立的线性约束条件来描述?
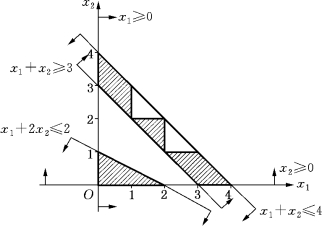
图5-2
解 如果阴影部分所表示的可行域用数学语言来描述,就是下列选择性约束条件:
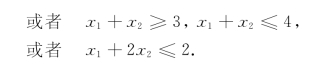
我们先引进第一级0-1变量y1,将它们表达为联立约束条件:
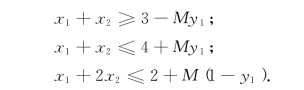
而当x1+x2≥3及x1+x2≤4成立(即y1=0)时,

我们引进第二级0-1变量y2、y3和y4,上述选择性约束条件(5-2)就成为
![]()
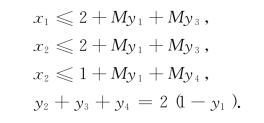
联立在一起,该可行域即描述为
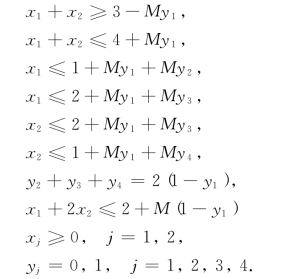
例5-5 (非线性整数规划问题线性化) 试将下列非线性整数规划变换成整数规划:
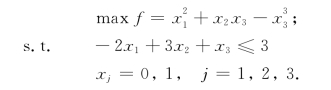
解法一 显然,对任k>0,0-1变量xj总有:xkj=xj,于是目标函数化成
![]()
我们引入0-1变量y来代替x2x3:
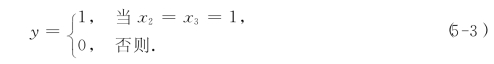
我们用下述两个约束条件来体现上述规定:

这是由于:当x2=x3=1时,约束条件(5-4)化成y≥1和y≤1,从而有y=1;当x2或x3中至少有一个为零时,由式(5-4)的第二个约束y≤![]() 得知y=0.
得知y=0.
从而,本模型化为
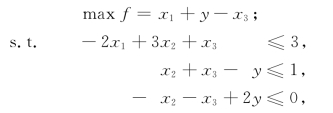
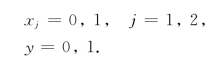
解法二 在方法一中每有一个0-1变量乘积项,就要引入一个整数变量,但计算机求解整数规划的时间随着整数变量个数增加而增加,为避免这种情况,我们引入非负连续变量y来代替x2x3,式(5-3)的规定用下列3个约束条件来体现:
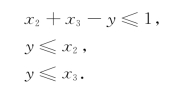
显然,当x2=x3=1时,这3个约束条件联立在一起,即可得出y=1;而当x2或x3至少有一个为零时,第二个或第三个约束条件迫使y=0.所以说,这3个约束条件隐含了y是0-1变量.
本模型化为
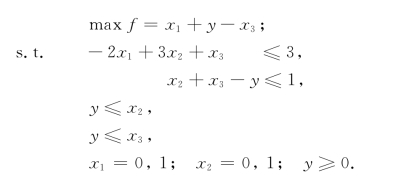
推而广之,当模型中出现k个0-1变量xj的乘积x1…xj…xk时,我们用下列两种方法处理:
方法一 引入0-1变量y取代乘积项x1x2…xk并增加下列两个约束条件:
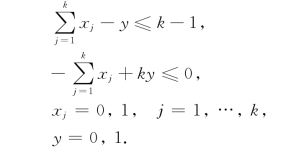
方法二 引入非负变量y代替乘积项x1x2…xk,并增加下列(k+1)个约束条件:
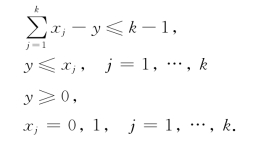
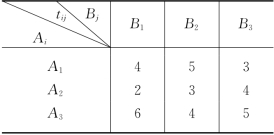
例5-6 (最优分配问题) 现有4部车床Ai(i=1,…,4)和4个零件Bj(j=1,…,4),车床Ai加工零件Bj所需时间tij(小时)由表5-1给出.问如何安排生产计划,使每部车床加工一个零件、一个零件由一部车床加工,且全部零件加工完成的时间最早(假定4部车床同时开始加工).试建立整数规划模型.
表5-1
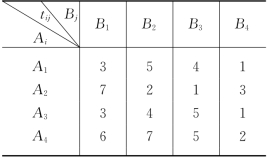
解 设0-1变量xij为

因为每部车床仅加工一个零件,所以有
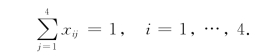
因为每个零件仅需一部车床加工,所以有
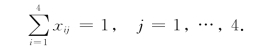
假设y为全部零件完工时间,则有
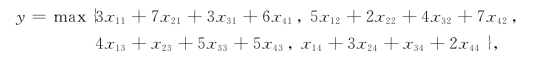
我们将它化为线性约束条件:
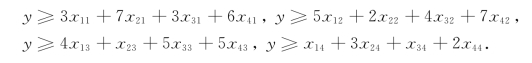
于是,得整数规划模型如下:
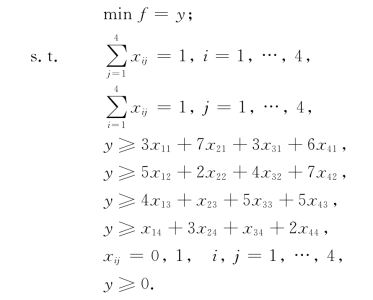
例5-7 (选址问题) 现准备从A1,A2,A33个地点选择两处开设工厂,它们每月的产量ai(i=1,2,3)分别至多为70,80和90个单位,每月的经营费用di(与产量无关)分别为100,90和120.有3家客户B1,B2和B3,它们每月的需求量bj(j=1,2,3)分别为40,60和45个单位.Ai至Bj的单位运价Cij(如表5-2所示).问如何选址,使每月经营和运输费用最低?试建立整数规划模型.
表5-2

又设xij为在地点Ai处开设工厂时从Ai至客户Bj的运量.
显然,有y1+y2+y3=2.
若在Ai处不开设工厂,则Ai至Bj的运量应为零;若在Ai处开设工厂,则每个月Ai至Bj的运量之和不超过Ai处开设工厂的产量ai,写成约束条件就成为
![]()
又客户Bj的需求量必须得到满足,所以有
![]()
每月的费用f为
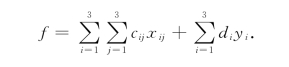
则本问题的数学模型为
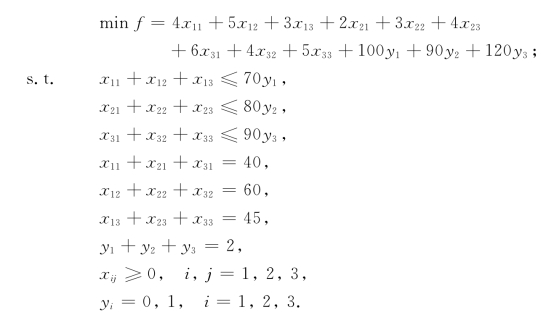
例5-8 (排序问题) 用编号为1#、2#、3#、4#的4种机床生产3种产品1#,2#,3#.这3种产品的工艺路线及工序加工时间如表5-3所示.一台机床一次只能加工一个产品.现要求2#产品从开始加工到完成,经历时间不得超过d小时.问如何确定各种产品在机床上的加工顺序,使在最短时间内制成全部产品.试建立整数规划模型.
表5-3
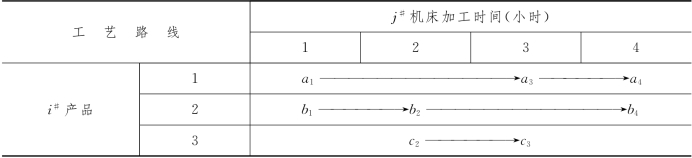
解 设xij为i#产品在机床j#上开始加工的时间(从零基准点算起,以小时计).
第一组约束条件为要求3种产品都应按照工艺路线的规定顺序来进行加工.例如对1#产品来说,首先是在1#机床上加工,然后依次在3#和4#机床上加工,因此有
![]()
类似地,对2#和3#产品,有
![]()
第二组约束条件为一族选择性的约束条件,以保证一台机床一次只能加工一个产品.例如,对于机床1#来说,或者1#产品先于2#产品加工,或者2#产品先于1#产品加工,即应有
![]()
引进0-1变量y1,上述选择性约束条件就成为
![]()
类似地,借助于0-1变量y2,y3和y4,对2#,3#和4#机床有
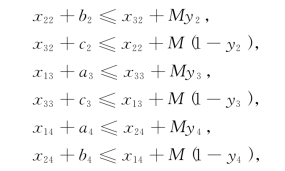
其中yj=0,1,j=2,3,4.
2#产品从1#机床对它开始加工(在x21时刻)到4#机床将其加工完毕(在x24+b4时刻),其经历时间有约束:
![]()
3个产品都完工的时间y为
![]()
我们将它化为线性约束条件
![]()
综上所述,得整数规划模型如下:
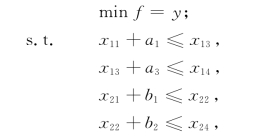
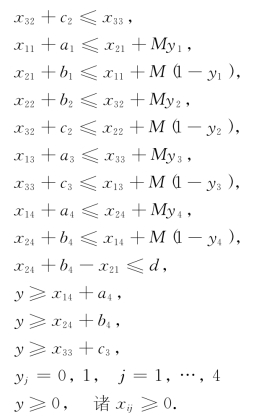
例5-9 (利润分段线性问题) 某厂生产甲、乙两种产品,需经过金工和装配两个车间加工,有关数据如表5-4所示.产品乙无论生产批量大小,每件产品生产成本总为400元.试根据产品甲生产成本的下列两种情况分别建立整数规划模型:
表5-4
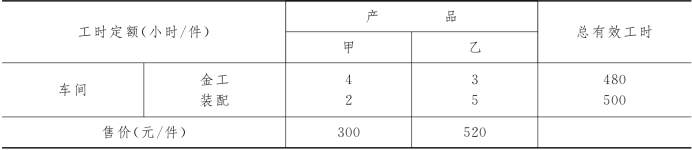
(1)产品甲的生产成本分段线性:第1件至第30件,每件成本为200元;第31件至第70件,每件成本为190元;从第71件开始,每件成本为195元.
(2)产品甲的产量不超过40件时,每件成本为200元,但若超过40件,则甲的全部产品每件成本都为195元.
解 设甲、乙产品的生产数量分别为x1,x2件.由表5-4知产品甲至多生产120件.(www.daowen.com)
(1)令x1=x3+x4+x5,其中x3、x4和x5满足下列约束条件:
当0≤x1≤30时,有
![]()
当30≤x1≤70时,有
![]()
当70≤x1≤120时,有
![]()
此时,产品甲所获利润为100x3+110x4+105x5,产品乙所获利润为120x2.
引进0-1变量y1和y2将上述约束条件(5-5)、(5-6)和(5-7)化成下列约束条件:
![]()
这时,如果y1=0,则必有y2=0,从而约束(5-5)成立;如果y1=1,y2=0,则有约束(5-6)成立;如果y1=1,y2=1,则有约束(5-7)成立;而y1=0,y2=1这是不可行的.
我们即得本问题的整数规划模型:
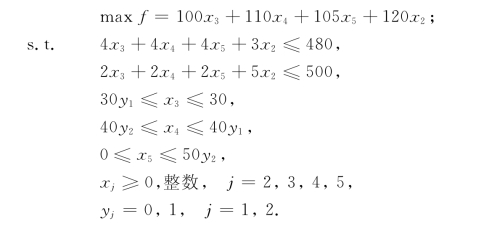
(2)令x1=x3+x4,其中x3,x4满足下列约束条件:
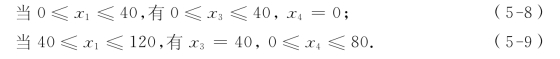
我们引进0-1变量y,将上列约束条件化成:
![]()
此时,如果y=0,则约束(5-8)成立,产品甲的利润为
![]()
如果y=1,则约束(5-9)成立,产品甲的利润为
![]()
综合这两种情况,可知产品甲的利润为
![]()
我们即得整数规划模型如下:
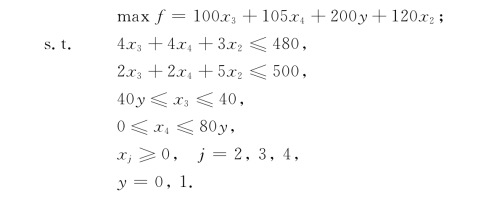
例5-10 (旅行售货员问题) 现有一位旅行售货员欲到城市v1,v2,…,vn进行商品销售.已知从城市vi到城市vj旅途所需时间为wij=W(vi,vj)(i≠j,i,j=1,…,n).今他从n个城市中的某一个城市出发,试问他应如何计划他的旅行路线,使他对每个城市恰好进行一次访问后又返回出发城市,而旅途所花费的时间最少?
解 设

因此,问题的目标函数为
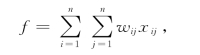
其中wii=M(充分大的正数).
由于旅行售货员在旅途中到达和离开每个城市恰好一次,因此,有约束条件:
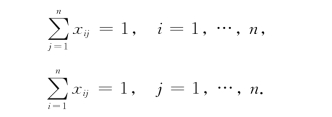
但是,满足这些约束条件的解不一定是旅行售货员的一条旅行路线.例如在一个6个城市的旅行售货员问题中,按上述约束条件定出的解,可能会形成两个分离的子回路,如图5-3所示.由于它们不是一个单一的回路,所以不能作为旅行售货员问题的一个可行解.
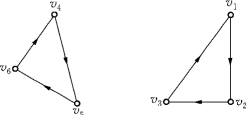
图5-3
为了避免出现多子回路的“分离”现象,必须追加一些约束条件.例如要防止n=6时旅行售货员问题出现图5-3这样的解,就可以附加下列约束条件:
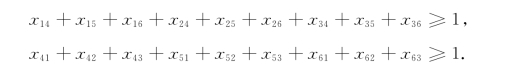
这两个不等式保证在旅行路线中把集合{v1,v2,v3}同集合{v4,v5,v6}联系起来.
因为旅行售货员问题要求任意两个城市vi和vj之间都应有相应的旅行路线把它们连接起来,所以,若把n个城市任意分成两组:{vi|i∈Q}及{vj|j∈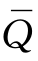 }(其中Q为{1,…,n}的非空真子集,
}(其中Q为{1,…,n}的非空真子集,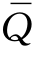 为{1,…,n}-Q),则在旅行路线中一定要存在以城市v
为{1,…,n}-Q),则在旅行路线中一定要存在以城市v
i(i∈Q)为起点、以城市vj(j∈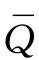 )为终点的一个行程.我们可以用下列约束条件来体现这个要求:
)为终点的一个行程.我们可以用下列约束条件来体现这个要求:
![]()
由于Q为{1,2,…,n}的任一非空真子集,共有2n-2个,因此这类附加的约束条件共有2n-2个.于是,我们得旅行售货员问题的0-1规划模型:
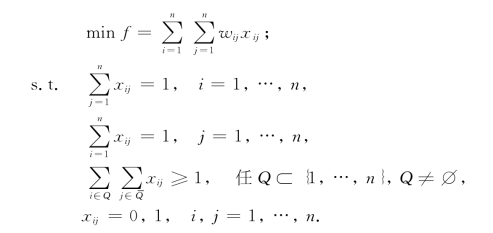
例5-11 (可靠性问题) 某种仪表由3个部件串联而成.j#部件的可靠性由所组装的j#元件个数决定,由表5-5给出;每个j#元件的重量和成本由表5-6给出.
表5-5
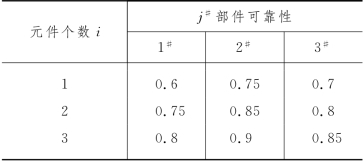
表5-6
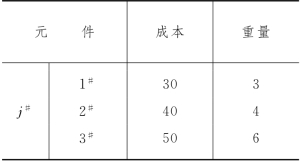
在设计过程中,该仪表对3个部件的总重量限制为25,总成本限制为240,问j#部件如何选择j#元件的个数,使仪表的可靠性最大?

考虑到j#部件或选1个,或选2个,或选3个j#元件,故有约束条件:

仪表的可靠性R=R1R2R3,它为非线性函数,取对数后即可得到一个线性函数,从而,目标函数为
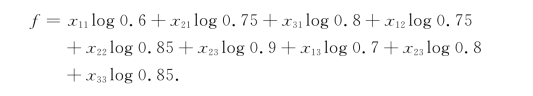
我们得到如下线性整数规划模型:
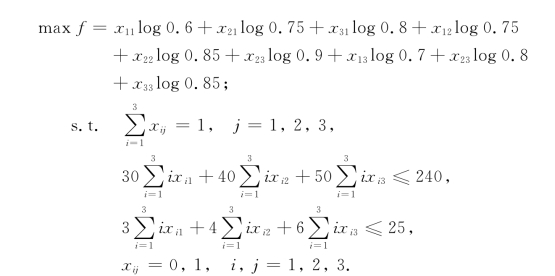
例5-12 (装配线平衡问题) 若某工厂的产品的装配线由6道工序组成,各工序的加工时间及工序的前后顺序如表5-7所示.
若这条装配线设若干个工作站.被装配的产品在这些编了号的工作站上流水移动时,每个工作站都要完成一道或几道工序.假设每个工作站加工每个被装配的产品时至多耗时10分钟,问最少应设立几个工作站?每个工作站完成哪些工序?
表5-7
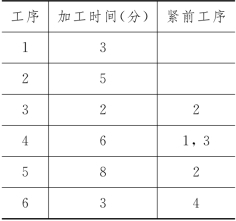
解 显然,需要的工作站不会多于4个.这是因为由表5-7可以观察到一个解:工序1,2,3在一个站上完成,而工序4、5和6各在一个工作站上进行,此时只需4个工作站.
令

因此,为使工作站数实现最少,目标函数为
![]()
接下来我们来分析约束条件:
第一组约束条件:对工序i来说,它应恰在某一个工作站上完成,为此有
![]()
第二组约束条件:对工作站j来说,在该站上完成的各道工序所需时间的总和不得超过10分钟,因此有
![]()
第三组约束条件:工作站j若设立,则在此站上完成的工序不会超过6道;若不设立,那么就不能将任何工序分派给该站(换句话说,若wj=0,则所有的xij=0),从而有
![]()
最后我们来考虑关于各道工序前后顺序这组约束条件:首先考虑工序2应当在工序3之前完成这个要求.若工序3在最后一个工作站4上完成,那显然没有什么问题,因为所有工序都要在此站前完成或就在此站上完成.若工序3分配在工作站3上完成,则工序2就不能分配在工作站4上完成,而必须分配在工作站1,2或3上完成,由此可得:
![]()
它说明,若x33=1,则x21,x22,x23中必有一个变量取值为1,以保证工序2在工序3之前完成.类似地,若工序3分配在工作站2或1上完成,则应分别有
![]()
同样地,对于工序表(表5-7)中列出的每个要求,都有3个(比工作站数少1)这样的约束条件:
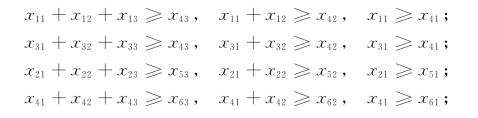
因此,对于6道工序、4个工作站、5个工序顺序制约要求的装配线平衡问题,我们建立的整数规划模型一共有28个变量及29个约束条件.可以想见,当一条装配线的工序个数、工作站数和工序顺序制约要求数很大时,为它建立的整数规划模型将是极其庞大的.
例5-13 (货物列车编组计划问题) 某铁路线路有5个货物列车编组站A1,A2,A3,A4和A5.编组站Ai发往前方各编组站Aj的车辆数aij(或称为车流量)已知,如图5-4所示.若始发站Ai至到达站Aj开行直达列车(按直达列车含义,应有j≥i+2),在Ai站就要消耗一个列车集结时间ci车小时(与车流量aij大小无关).又设在Ai站中转改编一辆车辆所花费的时间为ti小时.现制订列车编组计划的最优方案,以使车流集结和车辆改编的车小时总消耗达到最小.试建立整数规划模型.
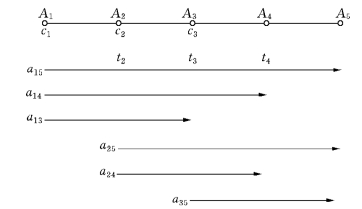
图5-4
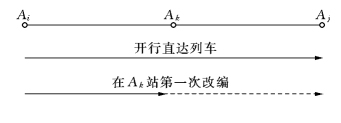
图5-5
解 根据铁路实际情况,相邻编组站之间的货物列车(称为直通列车)是一定开行的,所以对于目标函数来说,需开行的直通列车的集结时间之和是个常量,在求模型的最优解时,不妨把它们从目标函数f中略去.
由图5-5可知,车流aij可开行直达列车到达Aj站(j≥i+2);也可先开往Ak站并在Ak站第一次改编(到达Ak站后,如何继续开行,是否还有第二次改编,由Ak站决定.在Ak站改编的车流,应算作Ak站发出的车流).
令

又设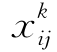 为Ai站开往Aj站的车流在Ak站第一次改编的车数(i<k<j).于是,目标函数f为
为Ai站开往Aj站的车流在Ak站第一次改编的车数(i<k<j).于是,目标函数f为
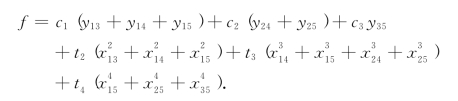
下面我们来讨论有关的约束条件.
第一组约束条件:考虑在A1站发出的车流.
若A1站至A5站开行直达列车,则必然包括车流a15的全部;否则,根据客观条件,只能在A2站、A3站、A4站之一第一次改编,因此有
![]()
由于车流a15仅可以在A2,A3和A4中一个站第一次改编,因此,引进3个0-1变量y1,y2和y3,并给出下列约束条件:
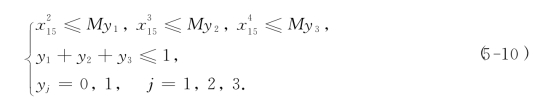
类似地,有
![]()

我们应注意到,式(5-14)是非线性约束条件.不难证明,对模型的最优解来说,它与下列线性约束条件是等价的:

由于我们的问题是求min f,且目标函数f中变量的系数都大于零,所以对最优解来说,必定有:


在这里,我们可以指出:若把上述建立的模型中的3组约束条件(5-10)、(5-12)和(5-15)删去,从数学上可以证明,所得的新模型在最优解上与原有模型是等价的.
一般来说,整数规划可以分成下列几种类型:
(1)纯整数规划,简记为(AIP):
![]()
(2)混合整数规划,简记为(MIP):
![]()
其中N1⊂{1,…,n};
(3)0-1规划:(LP)中X的分量或为0或为1,简记为(BIP).
在上述模型中,A=(aij)m×n,b=(b1,…,bm)T,C=(c1,…,cn)T,且aij,bi,cj均为整数(i=1,…,m;j=1,…,n).
我们可以指出,对于混合整数规划:
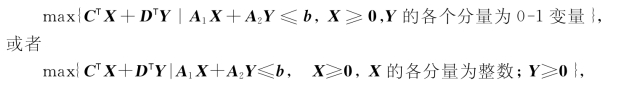
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






