第一章讨论的线性规划问题的决策变量都是连续型的，但是对某些实际问题而言，问题的全体或部分决策变量被限制为离散型的整数值，我们称这样的线性规划问题为整数线性规划，简称整数规划，简记为（IP）.

我们自然很容易地想到，若把整数规划的决策变量的整数约束去掉，得到相应的连续型变量的线性规划，对这个线性规划用单纯形法求解，然后将得到的最优解中要求取整数值的决策变量的值进行舍入处理，从而把所得结果作为整数规划的最优解.但是，实际例子告诉我们这个方法是不可行的.

例5－1　求解整数规划：

解　我们去掉上述问题中x1、x2为整数这个约束，得到相应的线性规划，用图解法进行求解（如图5－1），得到线性规划的最优解X＊＝（x1，x2）T＝（1.5，3.33）T，最优值为－4.83.

如图5－1所示，该整数规划的可行解集合是一些离散的点（今后我们仍用可行域来通称整数规划可行解的集合）.(www.daowen.com)

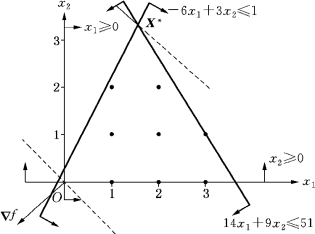
图5－1

如果我们对X＊的变量x1及x2分别作舍入处理，得到4个整数解：

（2，3）T，（1，3）T，（2，4）T，（1，4）T，我们发现，它们都不是整数规划的可行解.事实上，该整数规划的最优解是（2，2）T或（3，1）T.

另一方面，如果我们采用上述处理方法来求解（IP），那么，当（IP）有n个取整数值的变量时，则相应线性规划的最优解中，要求取整数值的变量的值都有舍或入两种可能，总共就有2n种可能的舍入方案.当n＝60时，260≈1018，这时即使应用高速电子计算机也难以处理全部舍入方案.所以，有必要对整数规划建立一些有效的算法.