为深刻理解目标规划模型及其相关基本概念，我们这里给出仅含有2个决策变量的目标规划的图解法.

例4－3　求解目标规划

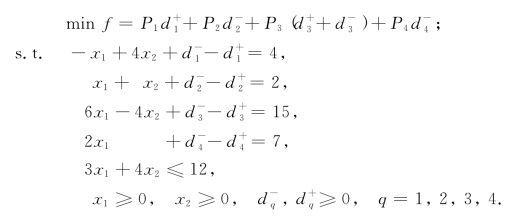
解　（1）在平面直角坐标系x1Ox2中，作出系统约束x1≥0，x2≥0，3x1＋4x2≤12所对应的可行域K，如图4－1中的三角形OEF所示.

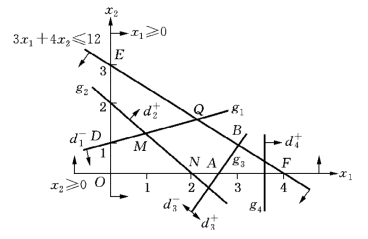
图4－1(www.daowen.com)

在这里我们要指出，上述Pt级目标的满意解对于低于Pt级的个别目标仍然有可能完全达成，详细讨论请参考有关目标规划的著作.

在目标规划模型（4－2）中存在着系统约束（假设它们是相容的），我们引进松弛变量或者剩余变量将它们化成等式约束.我们知道，对于模型（4－2），共有S个优先因子P1，P2，…，PS，表示各个目标分属不同的等级，这些目标之间存在一个定性的优先关系.如果将P1，P2，…，PS理解为不同等级的充分大的正数M1，M2，…，MS，定性关系“Pt≫Pt＋1”等价于“正数Mt充分大于Mt＋1”，那么f是关于偏差变量的线性函数，于是目标规划模型在形式上完全成为一个标准型的线性规划模型（LP），因而完全可以采用线性规划的单纯形法求解目标规划模型.只不过在采用单纯形法的求解过程中，必须明确“正数Mt充分大于Mt＋1”（t＝1，2，…，S）.也就是说，应该严格遵守目标规划“级别较高（同级权重较大）的目标优先实现，在其不退化的前提下，再考虑次级目标（同级权重较小）的实现”的求解原则.我们不再举例介绍目标规划的单纯形法，有兴趣的读者可以参阅相关的参考书.