在建立线性规划模型的基础上,我们建立目标规划模型的基本步骤为
①对各个目标确定目标期望值;
②对各个目标引进偏差变量,建立目标约束方程;
③确定目标优先等级和相对权重系数,建立达成函数.
这里,目标规划中的达成函数完全是由偏差变量、目标优先因子和相对权重系数组成的,这与线性规划中的目标函数是有区别的.
为了建立目标规划的一般数学模型,我们给出下面一些符号:
Q——目标规划中目标的个数;
Zq——第q个目标的目标函数Zq=![]() ,q=1,2,…,Q;
,q=1,2,…,Q;
Eq——第q个目标的目标期望值,q=1,2,…,Q;
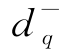 ,
,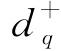 ——第q个目标约束引进的偏差变量,q=1,2,…,Q;
——第q个目标约束引进的偏差变量,q=1,2,…,Q;
Zq+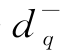 -
-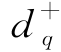 =Eq——第q个目标约束,q=1,2,…,Q;
=Eq——第q个目标约束,q=1,2,…,Q;
S——目标规划中目标的优先等级数;
P1,…,Pt,…,PS——目标优先因子,有P1≫…≫Pt≫…≫PS;
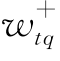 ,
,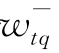 ——第q个目标的正负偏差变量在第t个优先级中的相对权重系数(这里,我们需要指出,在同一t优先级中一般仅包含数个目标,这些目标的正负偏差变量在该级达成函数中的相对权重系数至少有一个不为零,而那些不属于t优先级的目标,其正负偏差变量在该优先级中的相对权重系数均为零);
——第q个目标的正负偏差变量在第t个优先级中的相对权重系数(这里,我们需要指出,在同一t优先级中一般仅包含数个目标,这些目标的正负偏差变量在该级达成函数中的相对权重系数至少有一个不为零,而那些不属于t优先级的目标,其正负偏差变量在该优先级中的相对权重系数均为零);

对于上述目标规划问题,应严格按照“级别较高(同级权重较大)的目标优先实现,在其不退化的前提下,再考虑次级目标(同级权重较小)尽可能实现”的逐级优化原则进行求解.
例4-2 给出2个产地A1,A2,3个销地B1,B2,B3的不平衡运输问题如表4-2所示.产地A1,A2的物资必须全部运走.现有如下各级目标:
表4-2

P1——实际供应每个销地的数量均不超过其需求量;
P2——实际供应每个销地的数量至少要满足其需求量的75%;
P3——实际调运方案的总运费不超过当不考虑本例中其他各级目标时的最低总运费的1.1倍;
P4——基于合同规定,产地A2至少供应B1销地100个单位;
P5——基于运输安全的考虑,尽量减少A1向B3、A2向B2的调运量(该级目标的相对权重系数为A1至B3、A2至B2的单位运价之比);
P6——供给销地B1和B2的实际数量,各自与其需求量的比值应相等;
P7——总运输费用最小;(https://www.daowen.com)
试建立该运输问题的目标规划模型.
解 首先采用表上作业法求得最小运费调运方案如表4-3所示,总运输费用为150×10+150×4+400×3=3 300.
表4-3
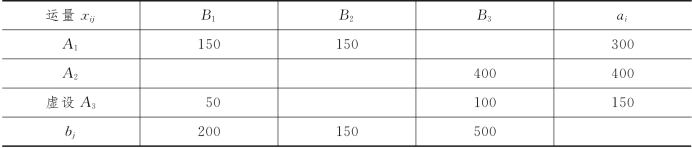
设xij为产地Ai调运至销地Bj的产品数量(i=1,2;j=1,2,3);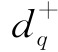 ,d-q为有关目标约束的正、负偏差变量,则有约束条件如下:
,d-q为有关目标约束的正、负偏差变量,则有约束条件如下:
(1)供应量约束:
![]()
(2)每个销地实现最高需求目标(P1级)的目标约束:
![]()
(3)每个销地实现最低需求目标(P2级)的目标约束:
![]()
(4)实现总运费目标(不超过最低运费3 300的1.1倍)(P3级)的目标约束:
![]()
(5)实现合同目标(P4级)的目标约束:
![]()
(6)实现安全目标(P5级)的目标约束:
![]()
(7)实现等比调入目标(P6级)的目标约束:
![]()
(8)实现总运费最低目标(P7级)的目标约束:
![]()
根据本运输问题的目标优先等级和具体要求,其达成函数表示如下:

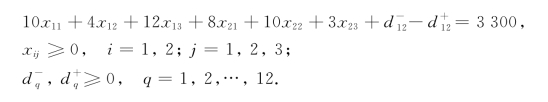
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






